Лабораторная работа: Определение оптимальной связывающей сети
Ошибки первого и второго вида система контроля не сможет исправить самостоятельно, их надо учесть заранее.
В задачи помехоустойчивого кодирования входит обнаружение и исправление ошибок третьего вида. Эта цель достигается введением избыточной информации. Избыточность информации можно получить аппаратными (схемными), логическими и информационными средствами. Существует несколько десятков разнообразных методов распознавания и коррекции ошибок кодирования, предназначенных для каналов связи с различными характеристиками помех.
Сформулируем три глобальные проблемы кодирования:
1) создание шифра кодирования;
2) создание специальных корректирующих кодов для поиска и исправления ошибок, возникающих в результате передачи и хранения информации;
3) минимизация избыточной информации для успешной коррекции и сокращения потерь в скорости передачи сообщения.
Один из самых эффективных путей кодирования основан на применении основной теоремы Шеннона для каналов без шума. Согласно первой теореме Шеннона, если канал передачи не содержит собственных помех, то, возможно, так закодировать сообщение, чтобы среднее число элементов кода (двоичных символов), приходящихся на один элемент кодируемого алфавита, было минимальным. Это так называемое эффективное статистическое кодирование.
Первая теорема Шеннона утверждает, что вероятность ошибок при передаче информации сколь угодно мала, если энтропия S множества передаваемых сообщений меньше пропускной способности канала связи С, определяемой как наибольшее число бит, которые возможно передавать по этому каналу связи за единицу времени.
Для каналов связи с помехами справедлива вторая теорема Шеннона (прямая теорема кодирования), согласно которой всегда существует способ кодирования, такой, что информация может быть передана с какой угодно высокой достоверностью при большой длине передаваемых слов, если скорость передачи не выше пропускной способности канала связи. Вторая теорема Шеннона доказывает принципиальную возможность помехоустойчивого кодирования.
Первый классификационный признак – коды бывают блочными или непрерывными. При блочном кодировании передаваемые двоичные сообщения сгруппированы в блоки, которыми кодируются знаки (или группы знаков) первичного алфавита. В блоке присутствуют информационные и проверочные биты. Если все кодовые комбинации имеют одинаковую длину, код называется равномерным; если нет – неравномерным. При декодировании удобнее (проще) иметь дело с равномерным кодом, поэтому именно он, как правило, используется в помехоустойчивом кодировании. Непрерывные (синонимы: цепные, сверточные, рекуррентные) коды представляют собой непрерывную последовательность бит, не разделяемую на блоки (информационные и проверочные биты в них чередуются по определенному правилу). Блочное кодирование удобно использовать в тех случаях, когда исходные данные по своей природе уже сгруппированы в какие-либо блоки или массивы. При передаче по радиоканалам чаще используется сверточное кодирование, которое лучше приспособлено к побитовой передаче данных. Кроме этого, при одинаковой избыточности сверточные коды, как правило, обладают лучшей исправляющей способностью.
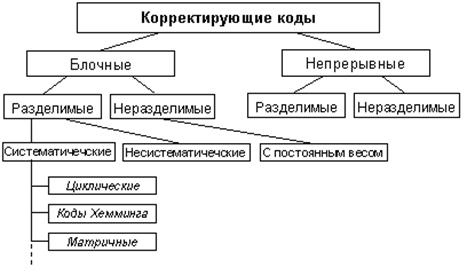
Рисунок 2 – Классификация помехоустойчивых кодов
Второй классификационные признак, относящийся как к блочным, так и к непрерывным кодам, подразделяет коды на разделимые и неразделимые. Разделимыми называются коды, в которых информационные и проверочные биты располагаются в строго определенных позициях. В неразделимых кодах такой определенности нет, что затрудняет их кодирование и декодирование. Поэтому практический интерес представляют в основном разделимые коды, а из неразделимых – только коды с постоянным весом.
Третий классификационный признак относится только к блочным разделимым кодам – они подразделяются на систематические (линейные) и несистематические. Двоичный код является линейным, если сумма по модулю 2 (mod2) двух кодовых слов также является кодовым словом этого кода. В линейных кодах проверочные биты являются результатом линейных операций над информационными разрядами. В несистематических (нелинейных) кодах информационные и проверочные биты либо вообще не имеют связи, либо эта связь нелинейна – такие коды применяются крайне редко.
Наиболее часто в линиях связи используются блочные линейные коды, называемые (n, k)-коды, к которым относятся циклические, коды Хемминга, матричные канонические и ряд других.
При цифровом кодировании дискретной информации применяют потенциальные и импульсные коды. В потенциальных кодах для представления логических единиц и нулей используется только значение потенциала сигнала. Импульсные коды позволяют представить двоичные данные либо импульсами определенной полярности, либо перепадом потенциала определенного направления.
При выборе метода цифрового кодирования к нему предъявляют следующие требования:
- наименьшая ширина спектра результирующего сигнала (узкий спектр сигналов позволяет добиваться высокой скорости передачи данных);
- возможность синхронизации между передатчиком и приемником (как правило, в сетях применяются самосинхронизирующиеся коды, сигналы которых позволяют передатчику автоматически определять тактовую частоту передачи информационных битов, например, по резким перепадам сигналов);
- возможность распознавания ошибок (распознавание и коррекция ошибок реализуется средствами логического кодирования, или используется избыточность физических кодов).
В самосинхронизирующихся кодах каждый переход уровня сигнала от высокого к низкому уровню или наоборот используется для подстройки приемника. Лучшими считаются коды, которые обеспечивают переход уровня сигнала не менее одного раза в течение интервала времени на приеме одного информационного бита.
Потенциальный код без возвращения к нулю (NRZ - Non Return to Zero) – 0 и 1 кодируются различными уровнями сигнала. Это наиболее простой способ кодирования, но имеет постоянную составляющую в спектре. При передаче длинных серий одноименных битов (единиц или нулей) уровень сигнала остается неизменным для каждой серии, что снижает качество синхронизации и надежность распознавания принимаемых битов.
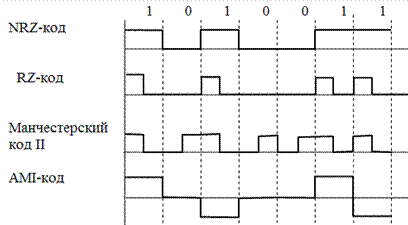
Рисунок 3 – Иллюстрация самосинхронизирующихся кодов
Потенциальный код с возвращением к нулю (Return to Zero) – код, аналогичный NRZ, с возвращением к нулю на середине каждого тактового интервала. Имеет большее число переходов уровня сигнала, чем сигнал в коде NRZ.
Биполярное кодирование с альтернативной инверсией (AMI) – 0 кодируется нулевым потенциалом, а 1 – положительным или отрицательным ненулевым, причем потенциал каждой следующей единицы противоположен по знаку предыдущей. Спектр кода не содержит постоянной составляющей. Используется три уровня сигналов, что требует увеличения мощности передатчика. Обладает хорошими синхронизирующими свойствами при передаче серий единиц и прост в реализации. Недостатком кода является ограничение на плотность нулей в потоке данных, поскольку