Лабораторная работа: Определение зависимости цены товара
2.Для проведения регрессионного анализа выполним:
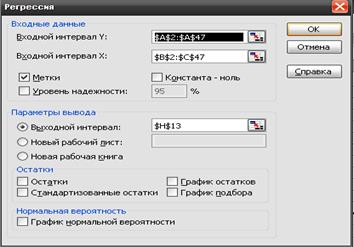
Команду Сервис – Анализ данных. В диалоговом окне выберем инструмент Регрессия, а затем ОК. В поле Входной интервал У введем адрес значений У из заданной таблицы. В поле Входной интервал Х – адрес значений Х.
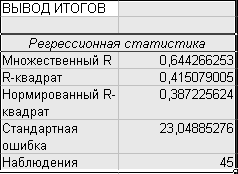
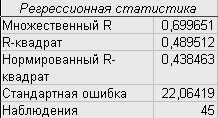
Данные регрессионного анализа:

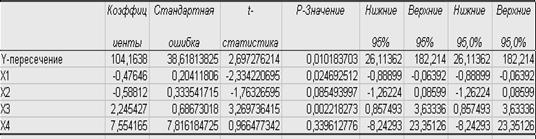
Запишем модель регрессии в линейной форме:
У=104,16 – 0,48Х1 – 0,59Х2 + 2,25Х3 + 7,55Х4
Оценим значимость факторов с помощью Т –критерия Стьюдента, для этого, определим его табличное значение при уровне значимости 0,05.
к = n-m-1=45-4-1=40 t-кр.таб=2.0211
Сравним расчетные значения с табличным по модулю:
│t X1= -2.334│ > t –табл. = 2,021,
следовательно фактор Х1(плотность) является статистически значимым, и статистически значимым признается влияние плотности колготок на их цену.
│t X2= -1,763│< t –табл. = 2,021,
следовательно фактор Х2 – содержание полиамида – является статистически незначимым.
│t X3= 3,269 │> t –табл. = 2,021,
следовательно фактор Х3 – содержание лайкры – является статистически значимым, и статистически значимым признается влияние содержания лайкры в колготках на их цену.
│t X4= 0,966 │< t –табл. = 2,021,
следовательно фактор Х4 – фирма-производитель – является статистически незначимым.
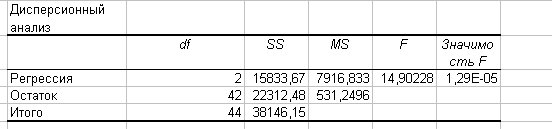
Оценка статистической значимости уравнения регрессии в целом осуществляется по F – критерию Фишера: Fтабл.= 2,61
Так как Fрасч. > Fтабл.(9,59 > 2.61), то уравнение регрессии можно признать статистически значимым (адекватным).
Оценка общего качества уравнения регрессии происходит с использованием коэффициента детерминации.
Так как R=0.489, то 48,9% вариации результативного показателя – цены колготок – объясняется вариацией факторных признаков, включенных в модель регрессии – плотность, содержание лайкры и полиамида, фирмы – производителя.
3.Постройте уравнение множественной регрессии только со статистически значимыми факторами. Рассчитайте доверительный интервал для каждого наблюдения, (уровень значимости примите равным 5%). Укажите торговые точки, в которых цены завышены.
| № | prise | DEN | lykra |
| Y | X1 | X3 | |
| 1 | 49,36 | 20 | 14 |
| 2 | 22,51 | 20 | 3 |
| 3 | 22,62 | 20 | 3 |
| 4 | 59,89 | 20 | 17 |
| 5 | 71,94 | 30 | 21 |
| 6 | 71,94 | 30 | 21 |
| 7 | 89,9 | 30 | 15 |
| 8 | 74,31 | 40 | 13 |
| 9 | 77,69 | 40 | 10 |
| 10 | 60,26 | 40 | 14 |
| 11 | 111,19 | 40 | 18 |
| 12 | 73,56 | 40 | 14 |
| 13 | 84,61 | 40 | 16 |
| 14 | 49,9 | 40 | 18 |
| 15 | 89,9 | 40 | 15 |
| 16 | 96,87 | 50 | 15 |
| 17 | 39,99 | 60 | 2 |
| 18 | 49,99 | 60 | 24 |
| 19 | 49,99 | 70 | 17 |
| 20 | 49,99 | 70 | 10 |
| 21 | 49,99 | 70 | 24 |
| 22 | 49,99 | 80 | 8 |
| 23 | 129,9 | 80 | 42 |
| 24 | 84 | 40 | 18 |
| 25 | 61 | 20 | 14 |
| 26 | 164,9 | 30 | 30 |
| 27 | 49,9 | 40 | 18 |
| 28 | 89,9 | 30 | 15 |
| 29 | 129,9 | 80 | 42 |
| 30 | 89,9 | 40 | 14 |
| 31 | 105,5 | 40 | 15 |
| 32 | 79,9 | 15 | 12 |
| 33 | 99,9 | 20 | 12 |
| 34 | 99,9 | 30 | 25 |
| 35 | 119,9 | 20 | 12 |
| 36 | 109,9 | 20 | 14 |
| 37 | 59,9 | 20 | 14 |
| 38 | 79,9 | 40 | 18 |
| 39 | 82,9 | 20 | 14 |
| 40 | 111,8 | 40 | 18 |
| 41 | 83,6 | 40 | 18 |
| 42 | 60 | 20 | 14 |
| 43 | 80 | 40 | 18 |
| 44 | 90 | 50 | 24 |
| 45 | 120 | 70 | 26 |
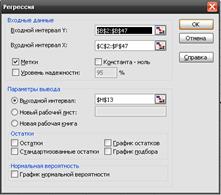
Эта операция проводится с помощью инструмента анализа данных Регрессия. В диалоговом окне при заполнении параметра входной интервал Х следует указать все столбцы.