Лабораторная работа: Поляризация электромагнитной волны

КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Институт радиоэлектроники и телекоммуникаций

Кафедра радиоэлектронных и телекоммуникационных систем

Лаборатория «Электродинамика и распространение радиоволн»

Лабораторная работа № ВИ-102

Поляризация электромагнитной волны

Казань, 2006 г.

Цель работы.

Целью работы является изучение поляризации электромагнитной волны и исследование с помощью виртуальной лабораторной установки различных видов поляризации.

Подготовка к работе.

Перед выполнением работы необходимо изучить соответствующий лекционный материал, настоящее описание и, при необходимости, рекомендованную литературу [1, с.57-59; 2, с.60-62; 3, с.158-162; 4, с.139-143; 5, с.180-187].

Краткие теоретические сведения.

В общем случае однородная плоская волна, которая распространяется в направлении оси z, имеет векторы и , лежащие в плоскости xOy фазового фронта. Эти векторы взаимно ортогональны, пропорциональны по величине и образуют с вектором Пойнтинга правую тройку векторов. Положение вектора в плоскости xOy может быть произвольным. Однако, вследствие того, что волна является гармонической с частотой и периодом колебаний , изменяющийся по величине и направлению вектор возвращается каждый период в исходное положение и рисует при этом своим концом на плоскости xOy замкнутую кривую, называемую годографом вектора . Вектор при этом однозначно определяется вектором и, при необходимости, всегда может быть найден.

Поляризация волны определяет закон изменения направления и величины вектора этой волны в данной точке пространства за период колебания. По форме годографа вектора определяют три вида поляризации монохроматических волн: линейная, круговая и эллиптическая.

Рассмотрим вектор , произвольно лежащий в плоскости xOy (рис.1):

. (1)

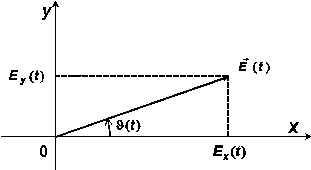
Рис.1. Вектор напряжённости электрического поля

Мгновенное значение модуля вектора

(2)

Угол вектора с осью x

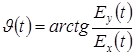(3)

Линейно поляризованной называют волну, у которой направление вектора остаётся неизменным с течением времени. Если начальные фазы суммируемых в выражении (1) ортогональных компонент поля совпадают или сдвинуты друг относительно друга на , то результирующая волна будет иметь линейную поляризацию. Действительно, подставив в (1) (где при и при ), имеем

, (4)

причем

. (5)

Из (5) следует, что

, (6)

и что направление колебаний вектора образует с осью x угол , который определяется соотношением

--> ЧИТАТЬ ПОЛНОСТЬЮ <--