Лабораторная работа: Представление сигналов в базисе несинусоидальных ортогональных функций
А = (a+b) (c+d)
которая требует выполнения лишь одной операции умножения и двух операций сложения.
Основная идея БПФ заключается в разделении исходной ![]() - точечной последовательности входных сигналов на две более короткие последовательности, ДПФ которых можно скомбинировать таким образом, чтобы получилось ДПФ исходной
- точечной последовательности входных сигналов на две более короткие последовательности, ДПФ которых можно скомбинировать таким образом, чтобы получилось ДПФ исходной ![]() - точечной последовательности. Так, например, если
- точечной последовательности. Так, например, если ![]() – четное, а исходная
– четное, а исходная ![]() - точечная последовательность разбита на две
- точечная последовательность разбита на две ![]() - точечные последовательности, то для вычисления искомого
- точечные последовательности, то для вычисления искомого ![]() - точечного ДПФ потребуется
- точечного ДПФ потребуется ![]() комплексных операций умножения, т.е. вдвое меньше по сравнению с прямым вычислением ДПФ. Здесь множитель
комплексных операций умножения, т.е. вдвое меньше по сравнению с прямым вычислением ДПФ. Здесь множитель ![]() равен числу умножений, необходимых для определения
равен числу умножений, необходимых для определения ![]() - точечного ДПФ, а множитель 2 соответствует двум ДПФ, которые должны быть вычислены. Эту операцию можно повторить, вычисляя вместо
- точечного ДПФ, а множитель 2 соответствует двум ДПФ, которые должны быть вычислены. Эту операцию можно повторить, вычисляя вместо ![]() - точечного ДПФ две
- точечного ДПФ две ![]() точечные ДПФ (предполагая, что
точечные ДПФ (предполагая, что ![]() – четное) и сокращая тем самым объем вычислений еще в два раза. Выигрыш в два раза является приблизительным, поскольку не учитывается, каким образом из ДПФ меньшего размера образуется искомое
– четное) и сокращая тем самым объем вычислений еще в два раза. Выигрыш в два раза является приблизительным, поскольку не учитывается, каким образом из ДПФ меньшего размера образуется искомое ![]() - точечное ДПФ.
- точечное ДПФ.
Функции Радемахера и их представление
Функции Радемахера составляют неполную систему ортонормированных функций, что ограничивает их применение. Но их широкое использование обусловлено тем, что на их основе можно получить полные функций, например, Хаара и Уолша. Непрерывная Функция Радемахера с индексом m, которая обозначается как rad(m,x), имеет вид последовательности прямоугольных импульсов, содержит ![]() периодов на полуоткрытом интервале [0;1) и принимает значения +1 или –1. Исключением является rad (0,x), которая имеет вид единичного импульса. Функции Радемахера периодические с периодом 1, т.е. rad(m,x) = rad(m,x+1). Кроме того, они периодические и на более коротких интервалах:
периодов на полуоткрытом интервале [0;1) и принимает значения +1 или –1. Исключением является rad (0,x), которая имеет вид единичного импульса. Функции Радемахера периодические с периодом 1, т.е. rad(m,x) = rad(m,x+1). Кроме того, они периодические и на более коротких интервалах: ![]() ,
, ![]() ,
, ![]() Их можно получить с помощью рекуррентного соотношения:
Их можно получить с помощью рекуррентного соотношения: ![]() ,
,
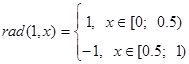
Получить функции Радемахера можно также с помощью следующего соотношения:
![]()
Первые четыре функции Радемахера представлены на рис.1.1 а, б
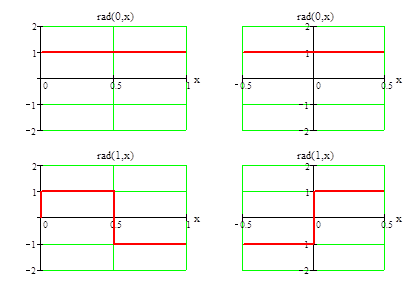
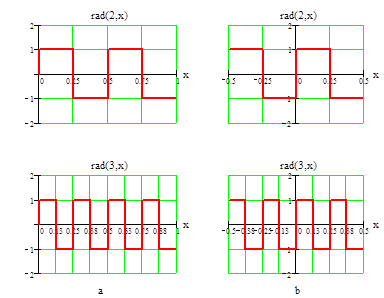
а) б)
Рис. 1.1. Первые четыре непрерывные функции Радемахера:
a) на интервале [0; 1); б) на интервале [-0.5; 0.5);
Пример разложения функции f(x) в базисе функций Радемахера, используя общую формулу (1.2) представлен на рис 1.2.
![]() , (1.2)
, (1.2)
где 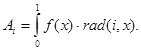
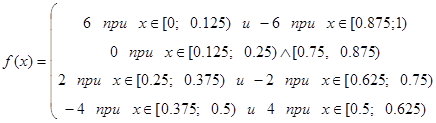
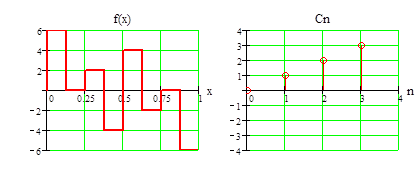
Рис.1.2. Пример разложения в базисе функций Радемахера.
Дискретные функции Радемахера
Дискретные функции Радемахера являются отсчетами непрерывных функций Радемахера. Каждый отсчет расположен в середине связанного с ним элемента непрерывной функции. Обозначаются дискретные функции Радемахера как Rad(m,x). Для дискретных функций Радемахера удобно использовать матрицу, каждая строка которой является дискретной функцией Радемахера. Например, для третьей диады (m=3) имеем: (для удобства обозначим “+1” как “+”, а “–1” как “–” )
|
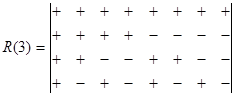
![]()
Функции Хаара и их представление
Множество непрерывных функций Хаара ![]() составляет периодическую, ортонормированную и полную систему функций. Широкое распространение функции Хаара получили в вэйвлет-анализа и сжатии изображений. Рекуррентное соотношение, которое дает возможность сформировать непрерывную функцию
составляет периодическую, ортонормированную и полную систему функций. Широкое распространение функции Хаара получили в вэйвлет-анализа и сжатии изображений. Рекуррентное соотношение, которое дает возможность сформировать непрерывную функцию ![]() , имеет вид:
, имеет вид:
![]()
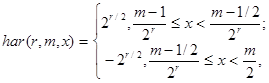
где ![]() и
и ![]() , N – общее количество функций.
, N – общее количество функций.