Лабораторная работа: Представление сигналов в базисе несинусоидальных ортогональных функций

Рис.1.3. Первые восемь непрерывных функции Хаара.

Дискретные функции Хаара

По аналогии с дискретными функциями Радемахера дискретные функции Хаара являются отсчетами непрерывных функций Хаара. Каждый отсчет расположен в середине связанного с ним элемента непрерывной функции. Обозначаются дискретные функции Хаара как .

Построим матрицу дискретных значений функций Хаара для 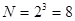, в которой каждая строка отвечает соответствующей функции.

Нar(0,0,x) Har(0,1,x) Har(1,1,x) Har(1,2,x) Har(2,1,x) Har(2,2,x) Har(2,3,x) Har(2,4,x)

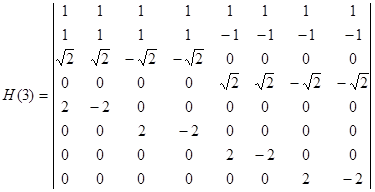
При цифровой обработке сигналов, вэйвлет-анализе, сжатии изображений, анализе и синтезе логических функций, часто применяются ненормированные функции Хаара, которые на отдельных участках принимают одно из трех значений +1; 0; –1.

Преобразование Хаара

Любую интегрируемую на интервале функцию можно представить рядом Фурье по системе функций Хаара:

, где (1.3)

с коэффициентами

. (1.4)

Домашнее задание

1. Выражения для непрерывных функций Радемахера

2.Матрица для системы дискретных функций Радемахера при N = 5.

Rad(0,t)	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1
Rad(1,t)	1	1	1	1	1	1	1	1	1	1	1	1	1	1	1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1	-1
Rad(2,t)	1	1	1	1	1	1	1	1	-1	-1	-1	-1	-1	-1	-1	-1	1	1	1	1	1	1	1	1	-1	-1	-1	-1	-1	-1	-1	-1
Rad(3,t)	1	1	1	1	-1	-1	-1	-1	1	1	1	1	-1	-1	-1	-1	1	1	1	1	-1	-1	-1	-1	1	1	1	1	-1	-1	-1	-1
Rad(4,t)	1	1	-1	-1	1	1	-1	-1	1	1	-1	-1	1	1	-1	-1	1	1	-1	-1	1	1	-1	-1	1	1	-1	-1	1	1	-1	-1
Rad(5,t)	1	-1	1	-1	1	-1	1	-1	1	-1	1	-1	1	-1	1	-1	1	-1	1	-1	1	-1	1	-1	1	-1	1	-1	1	-1	1	-1

3. Графики функций от до .

4. Выражение для нормированных функций Хаара.