Лабораторная работа: Распределения предприятий по прибыли от продаж

η = √0,95=0,975

Это говорит о том, что корреляционная связь играет существенную роль между затратами и суммой прибыли.

Задача № 3

По результатам выполнения задания 1 с вероятностью 0,683 определите:

1. Ошибку выборки средней суммы прибыли от продаж и границы, в которых будет находиться средняя сумма прибыли в генеральной совокупности.

2. Ошибку выборки доли организаций с суммой прибыли 14,948 млн. руб. и более и границы, в которых будет находиться генеральная доля.

Решение:

Определяем ошибку выборки (выборка механическая) для средней суммы прибыли на одно предприятие по следующей формуле:

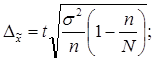
если Р=0,683, то t=1. Т.к. выборка механическая 20%-ная, то N=150

Δ_х =1*√(15,472/30)*(1-30/150)=0.7млн. руб.

Ошибка выборки для средней суммы прибыли на одно предприятие Δ_х =0,7млн.руб.

Средняя сумма прибыли будет находиться в границах которые мы находим по формуле :

8,301- 0,7≤ ≤8,301+0,7

7,601≤ ≤9.001

С вероятностью 0,683 можно утверждать, что средняя сумма прибыли одного предприятия заключается в пределах от 7,601 млн. руб. до 9,001 млн. руб.

Доля предприятий со средней прибылью свыше 16,6 млн.руб. находится в пределах :

Выборочная доля составит:

w =3/30=0,1 или 10%

Ошибку выборки определяем по формуле:

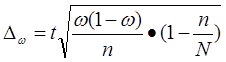где N-объем генеральной совокупности. Т.к. выборка 20%-ная и в выборку вошло 30 предприятий, то N=150.

Подставляя данные в формулу, получим:

D_w =1√(0,1(1-0,1)/30)*(1-30/600)

∆_w =0,0024

Следовательно с вероятностью 0,683 можно утверждать, что доля предприятий со средней прибылью > 14,948 млн. руб. будет находиться в следующих пределах:

0,1-0,0024≤∆_ω ≤0,1+0,0024

0,098≤∆_ω ≤0,1024

или от 9,8% до 10,24%.

Задача №4