Цель работы: Получить навыки описания метода решения математической модели на примере решения задач аналитической геометрии.

Задание: 1) Согласно заданному варианту описать методы решения задачи.

2) На основе описанных методов разработать математическую модель.

Задача: Задано множество точек, найти параметры окружности минимального радиуса, проходящие через три точки множества.

Ход работы

І)Математическая постановка задачи:

1) Найти наименьший радиус окружности по формуле: i : = 1…n

D=, где ;

j : = 1… 2)D1,D2,D3- радиусы окружности;

3) XY, XY, XY, XY- координаты точек множества;

4) D=-формула нахождения расстояния между двумя точками;

5)

-система уравнения или неравенства;

6)

-совокупность уравнения или неравенства;

7) -знак больше

-знак меньше

=-знак равно;

8) A, B, C, E- некоторые точки с определенными координатами

ІІ) Описание методов решения:

Метод 1. Метод заключается в том , что бы найти наименьший радиус окружности с помощью последовательного соединения точек с одной, а затем проделывания этого с каждой из точек множества. Затем, с помощью формулы нахождения расстояния между двумя точками

(D=),необходимо вычислить длины получившихся отрезков. После вычисления отрезки необходимо сравнить между собой. В результате если два отрезка, выходящие из одной точки, равны - это и есть радиусы окружности. Но из условия, поставленные задачей, необходимо найти минимальный радиус окружности проходящей через три точки множества. Если при сравнении несколько пар одинаковых отрезков - необходимо найти наименьшую пару – это и будет минимальный радиус окружности. (Рис.№1)

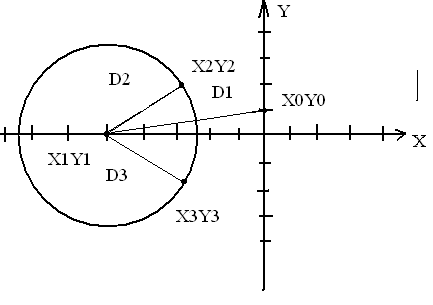
Рис.№1

Метод 2.Второй метод заключается в том, что бы искать минимальный радиус окружности при помощи соединения множество точек между собой, и в результате получение множество геометрических фигур ( в данном случае геометрические фигуры – треугольники). Затем необходимо найти расстояние сторон треугольника. Для этого возьмем формулу нахождения расстояния между двумя точками (D=). В случаи, если стороны выходящие из одной точки равны – это и есть радиусы окружности, так как через равные отрезки, выходящие из одной точки можно провести окружность с центром точки соединения этих отрезков. В случае, если в конечном результате вычисления несколько равных сторон, выходящих из одной точки, необходимо найти минимальный радиус окружности. Минимальным радиусом будут стороны с наименьшей длиной (рис.№ 2).

ІІІ) Анализ метода решения:

Первый метод более эффективен, чем второй, так как требует меньшее количество арифметических расчетов, и в памяти будет занимать меньшее количество ресурсов.

ІY) Формализация выбранного метода:

1) D1=

D2=

--> ЧИТАТЬ ПОЛНОСТЬЮ <--