Лабораторная работа: Транспортные модели
Лабораторная работа №4
Транспортные модели
Цель работы: научиться находить оптимальное решение задач транспортного типа.
Задание
Вариант 1. На четырех ткацких станках с объемом рабочего времени 200, 300, 250 и 400 станко-ч за 1 час можно изготовить соответственно 260, 200, 340 и 500 м ткани трех артикулов I, II, III. Составить оптимальную программу загрузки станков, если прибыль (в ден. ед.) от реализации 1 м ткани i-го артикула при ее изготовлении на j-м станке характеризуется элементами матрицы
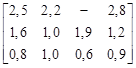 ,
,
а суммарная потребность в ткани каждого из артикулов равна 200, 100 и 150 тыс. м, учитывая, что ткань Iартикула не может производиться на третьем станке.
Табличная модель:
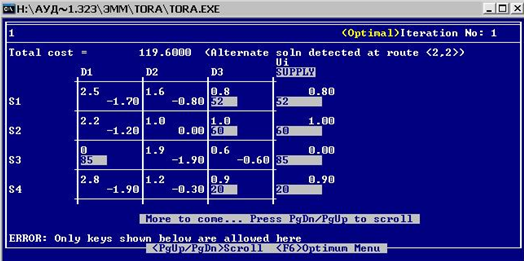
Контрольные вопросы:
1. Как записывается математическая модель задачи транспортного типа?
Обозначим через xij объем перевозок от i-го поставщика j-ому потребителю. Математическая модель задачи имеет вид:
1) объем поставок i-го поставщика должен равняться количеству имеющегося у него груза
![]() ;
;
2) объем поставок j-ому потребителю должен быть равен его спросу
![]() ;
;
3) объемы поставок должны выражаться неотрицательными числами
xij ³0; ![]() ,
, ![]() ;
;
4) общая сумма затрат на перевозку груза должна быть минимальной
![]() .
.
Если суммарный объем отправляемых грузов равен суммарному объему потребностей в этих грузах по пунктам назначения
![]() ,
,
то такая транспортная задача называется закрытой (сбалансированной), в противном случае — открытой (несбалансированной).
Если указанные затраты неизвестны (не указаны) соответствующие значения сij полагают равными нулю.
модель поставка потребность затрата
2. Как свести открытую транспортную задачу к закрытой?
Если имеет место открытая транспортная задача, ее необходимо свести к закрытой:
1) в случае перепроизводства – ввести фиктивного потребителя с необходимым объемом потребления (элементы матрицы сij , связывающие фиктивные пункты с реальными, имеют значения, равные затратам на хранение невывезенных грузов);
2) в случае дефицита – ввести фиктивного поставщика с недостающим объемом отправляемых грузов (элементы матрицы сij , связывающие фиктивные пункты с реальными, имеют значения, равные штрафам за недопоставку продукции).
--> ЧИТАТЬ ПОЛНОСТЬЮ <--