Лабораторная работа: Тривимірні перетворення

Вступ

Для кращого сприйняття форми об'єкта необхідно мати його зображення в тривимірному просторі. У багатьох випадках наочне представлення про об'єкт можна одержати шляхом виконання операцій обертання і переносу, а також побудови проекцій. Введемо однорідні координати. Точка в тривимірному просторі задається чотиримірним вектором чи . Перетворення з однорідних координат описується співвідношеннями

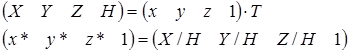( 4 .1)

де T - деяка матриця перетворення.

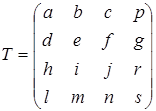
Ця матриця може бути представлена у вигляді 4 окремих частин

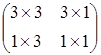
Матриця 3x3 здійснює лінійне перетворення у виді зміни масштабу, зсуву й обертання. Матриця-рядок 1х3 робить перенос, а матриця-стовпець 3х1 - перетворення в перспективі. Останній скалярний елемент виконує загальну зміну масштабу. Повне перетворення, отримане шляхом впливу на вектор положення матрицею 4x4 і нормалізації перетвореного вектора, будемо називати білінійним перетворенням. Воно забезпечує виконання комплексу операцій зсуву, часткової зміни масштабу, обертання, відображення, переносу, а також зміни масштабу зображення в цілому.

Тривимірна зміна масштабу

Діагональні елементи основної матриці перетворення 4х4 здійснюють часткову і повну зміну масштабу. Розглянемо перетворення

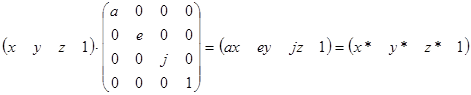,( 4 . 2 )

яке робить часткову зміну масштабу. На рис.4.1а показане перетворення паралелепіпеда в одиничний куб шляхом зміни масштабу. Загальна зміна масштабу виходить за рахунок використання четвертого діагонального елемента, тобто

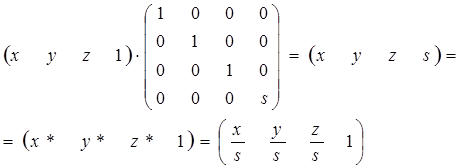. ( 4 . 3 )

Це перетворення ілюструє рис.4.1б. Такий же результат можна отримати при рівних коефіцієнтах часткових змін масштабів. У цьому випадку матриця перетворення повинна бути рівна

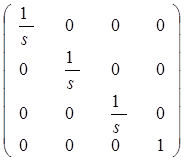. ( 4 . 4 )

Вектори положення точок А і В рівні і .

Рис.4.1. Тривимірні перетворення iз зміною масштабів.

Тривимірний зсув

Недіагональні елементи верхньої лівої підматриці 3х3 від загальної матриці перетворення розміру 4х4 здійснюють зсуви в трьох вимірах, тобто

. ( 4 . 5 )

Простий тривимірний зсув одиничного куба показаний на рис.4.1в.

Тривимірні обертання

Раніше було показано, що матриця 3х3 забезпечувала комбінацію операцій зміни масштабу і зсуву. Однак, якщо визначник матриці 3х3 дорівнює +1, то має місце чисте обертання навколо початку координат. Перед розглядом загального випадку тривимірного обертання навколо довільної осі дослідимо кілька окремих випадків. При обертанні навколо осі х розміри уздовж осі х не змінюються. Таким чином, матриця перетворень буде мати нулі в першому рядку і першому стовпці, за винятком одиниці на головній діагоналі. Це приводить до матриці перетворення, що відповідає повороту на кут навколо осі х і задається співвідношенням

( 4 . 6 )

Обертання вважається додатнім, тобто за годинниковою стрілкою, якщо дивитися з початку координат вздовж осі обертання. На рис.4.2а показаний поворот на -90° навколо осі x .

Для обертання на кут Ф навколо осі y - нулі ставлять у другому рядку і другому стовпці матриці перетворення, за винятком одиниці на головній діагоналі. Повна матриця задається виразом

( 4 . 7 )

--> ЧИТАТЬ ПОЛНОСТЬЮ <--