Научная работа: Построение маршрута при групповой рассылке сетевых пакетов данных
Для разбиения множества всех абонентов на подмножества не существует точных методов, но для конкретной задачи можно выработать специальный алгоритм на основе известных методов. При этом следует рассмотреть разные виды структур сетей (радиальные, древовидные), чтобы иметь возможность наиболее эффективно их комбинировать.
Второй этап алгоритма – это построение деревьев внутри каждой подсети. В качестве критериев обычно рассматривается время передачи единицы данных по каналу, расстояние или денежный эквивалент данного соединения, пропускная способность канала и др.
Для решения такой задачи существует множество чисто математических методов, но при достаточно большом числе абонентов они не всегда удобны. В реальных разветвленных сетях часто используют эвристические методы.
Но, так же как и для предыдущего этапа, универсального решения не существует. Поэтому следует рассмотреть различные методы построения деревьев и возможности их комбинирования.
Задача разработки программного продукта состоит в том, чтобы он предоставлял необходимые возможности. А именно: возможность создания и редактирования сети; визуализация схемы построенного маршрута; вывод результатов расчетов для пересылки по построенному маршруту; возможность настраивать параметры алгоритма для получения наиболее оптимального результата и др.
Сложность генетических алгоритмов при построении деревьев состоит в кодировке исходных данных. Для требуемых вычислений и представления структуры сети на экране используются различные типы данных. Поэтому предполагается совмещать вещественное представление хромосом с традиционным.
2 МЕТОДЫ СИНТЕЗА СТРУКТУРЫ СЕТИ
2.1 Размещение центров и синтез абонентских СДО в классе
радиальных структур
Точные методы для общей задачи структурного синтеза сетей неизвестны, однако для задач специального вида можно разработать алгоритмы, использующие, например, метод ветвей и границ.
2.1.1 Метод ветвей и границ
Этот метод является универсальным методом дискретной оптимизации и включает следующие процедуры: задание исходного множества вариантов, выбор наиболее перспективного множества для разбиения, ветвление множества на подмножества, определение нижней границы значения критерия на каждом из образовавшихся подмножеств, поиск допустимого решения в каждом из образованных подмножеств, проверку признака оптимальности. Основная трудность метода ветвей и границ состоит в выборе способа ветвления (разбиения) множества на подмножества и задании эффективной нижней границы критерия, позволяющей отбрасывать большое число бесперспективных вариантов.
Рассмотрим реализацию метода ветвей и границ для задачи размещения центров и синтеза радиальной структуры сети. Метод состоит из конечного числа однотипных итераций, на каждой из которых строится совокупность подмножеств вариантов:
![]()
где к — номер итерации.
Каждое из подмножеств ![]() характеризуется следующими множествами:
характеризуется следующими множествами: ![]() — множество пунктов, где РЦ уже построены;
— множество пунктов, где РЦ уже построены; ![]() — множество пунктов, где еще можно строить РЦ;
— множество пунктов, где еще можно строить РЦ; ![]() — множество пунктов, где наложен запрет на строительство РЦ, при этом
— множество пунктов, где наложен запрет на строительство РЦ, при этом
![]()
где Y — исходное множество пунктов, в которых допускается строительство РЦ, Y Є Х.
Обозначим через Xyi множество абонентов, подключенных к РЦ уi (у Є Р) по критерию минимума затрат на связь, т. е. х Є Хуi, если ![]() . Каждое из множеств
. Каждое из множеств ![]() характеризуется величиной нижней границы критерия
характеризуется величиной нижней границы критерия ![]() для всех структур (решений), определяемых данным множеством. Величина ξ задается следующим соотношением:
для всех структур (решений), определяемых данным множеством. Величина ξ задается следующим соотношением:
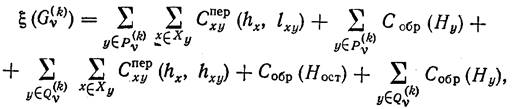
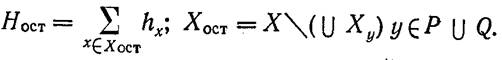
где.
Допустим, что каким-то приближенным методом (например, R-структур) удается построить структуру Х0 на множестве ![]() . При этом в решение должны войти все РЦ уiЄ
. При этом в решение должны войти все РЦ уiЄ![]() и не должно быть ни одного РЦ уiЄ
и не должно быть ни одного РЦ уiЄ![]() .
.
Обозначим величину критерия для структуры Х0 через W(Х0). Справедлив следующий признак оптимальности: если W(Х0) = ![]() , то вершина дерева решений
, то вершина дерева решений ![]() является конечной и дальнейшему разбиению не подлежит; если W(Х0) ≤ min
является конечной и дальнейшему разбиению не подлежит; если W(Х0) ≤ min ![]() для всех висячих вершин
для всех висячих вершин ![]() построенных на k-й итерации, то Х0 — искомое оптимальное решение (структура). Предположим, что уже проведено k итераций и еще не найдено оптимальное решение. Опишем произвольную (k + 1)-ю итерацию:
построенных на k-й итерации, то Х0 — искомое оптимальное решение (структура). Предположим, что уже проведено k итераций и еще не найдено оптимальное решение. Опишем произвольную (k + 1)-ю итерацию:
1.Среди всех множеств ![]() , построенных в результате k-й итерации, выбираем наиболее перспективное множество
, построенных в результате k-й итерации, выбираем наиболее перспективное множество ![]() , т. е. такое, что
, т. е. такое, что
![]() .
.
2.Ветвление. Выбираем некоторый РЦ yr Є![]() и разбиваем
и разбиваем ![]() на два подмножества
на два подмножества ![]() и
и ![]() так, что на подмножестве
так, что на подмножестве ![]() РЦ yr, переводится в разряд действующих, а на подмножестве
РЦ yr, переводится в разряд действующих, а на подмножестве ![]() накладывается запрет на строительство РЦ в пункте уr. Таким образом,
накладывается запрет на строительство РЦ в пункте уr. Таким образом,
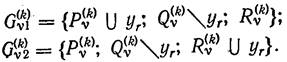
Будем выбирать уrтак, чтобы подмножество ![]() с наибольшей вероятностью содержало искомое решение, а
с наибольшей вероятностью содержало искомое решение, а ![]() не содержало. Тогда
не содержало. Тогда
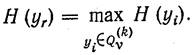
3.Вычисление оценок ![]() и
и ![]() . В частности, для множества
. В частности, для множества ![]() можно использовать следующую рекуррентную формулу:
можно использовать следующую рекуррентную формулу:
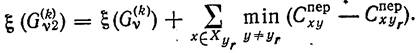 |
4.На каждом из подмножеств ![]() и
и ![]() находим допустимое решение, которое обозначим
находим допустимое решение, которое обозначим ![]() и
и ![]() соответственно.
соответственно.
5. Проверка признака оптимальности. Пусть ![]() ≤
≤ ![]() . Если
. Если