vt= a(bci0 + (l — b)ci2),

где ci0, ci2 — стоимости соединения терминала i с центральным узлом и с его ближайшим соседним терминалом соответственно; а и b— некоторые константы, причем а ≥ 0, 0 ≤ b ≤ 1. При а = 0 получаем алгоритм Краскала; при а = b = 1 — алгоритм Исау — Вильямса; при а = 1, b = 0 — алгоритм Фогеля. Наконец, придавая а и b некоторые промежуточные значения, можем получить одновременно свойства всех вышеперечисленных алгоритмов.

На практике обычно параметрам а и b придают некоторые начальные значения и затем, варьируя их по очереди и оценивая получаемые результаты, последовательно приближаются к наилучшему. Такой способ позволяет получить результаты на 1—5 % лучше, чем при использовании алгоритмов Исау— Вильямса и Фогеля. Указанный способ параметризации можно применять для одновременного решения задач группирования и размещения терминалов, если в выражении для vi под сi0 понимать стоимость соединения терминала i с ближайшим центральным узлом. При этом никакого предварительного разбиения терминалов на группы не производится, а оно выполняется автоматически в процессе работы алгоритма.

Рассмотрим эффективность реализации унифицированного алгоритма синтеза КСД. Сложность алгоритма — время вычислений и необходимый объем памяти — зависит от размерности графа N. В общем случае граф должен быть полным, что требует просмотра всех пар узлов. Однако при большом количестве терминалов можно без значительного снижения точности результатов решать задачу с помощью разреженного графа, в котором каждый терминал связан лишь с некоторым ограниченным числом соседних терминалов. Например, в сети с 40 узлами достаточно рассматривать соединения каждого терминала с пятью соседними. Дальнейшее увеличение числа терминалов К лишь незначительно улучшает результаты. Для сети терминалов, однородно распределенных вокруг центрального узла, можно игнорировать около 75 % возможных соединений. Для быстрой оценки приближенного значения К всю область, содержащую терминалы, разбивают на прямоугольники, в пределах каждого из которых находят К ближайших соседей заданного терминала. Благодаря такому правилу число операций для повторного вычисления Eij при включении новой ветви в дерево можно снизить с N (N — 1)/2 до N х К. Кроме того, учитывая, что Еij =vi-cij, где cij— константа, пересчет Еijможно свести к пересчету vi, т. е. вместо N х К повторных вычислений Eij достаточно пересчитать N раз значение vi.

В общем случае сложность алгоритма оценивается выражением: AN2 + BKN + CKN log2K, где А ,В и С — константы. При этом предполагается, что программа обеспечивает возможность реализации любого правила v. Однако, если правило v таково, что не требуется пересчет vi для каждого терминала, то членом AN2 можно пренебречь. Для многих практических целей сложность алгоритма имеет вид BKN + CKN log2К. Время работы ЭВМ и требуемый объем оперативной памяти при реализации алгоритма экспериментально оценены в сетях, содержащих 20, 40, 60, 80, 120, 200 узлов при учете только пяти соседних терминалов, использовании правила изменения v по алгоритму Исау — Вильямса и суммарном графике в ветви, ограниченном значением Н ≤ N/4.

Результаты экспериментов показали, что зависимость логарифма времени работы ЭВМ от логарифма числа терминалов имеет линейный характер с наклоном кривой, который свидетельствует о квадратичной зависимости вычислительной сложности унифицированного алгоритма от размерности задачи N. В результате исследований выявлено, что время решения задачи почти не изменяется при переходе от одного правила v к другому и при изменении ограничений, в то же время оно сильно зависит от числа соседних терминалов, подключаемых к данному (т. е. числа новых линий, подключаемых к дереву). Зависимость времени работы унифицированного алгоритма синтеза КСД от числа соседних терминалов для сети с 40 терминалами приведена в таблице 2.2.

Таблица 2.2 – Зависимость времени работы терминала

Число соседних терминалов, К	Время работы алгоритма, мин	Относительная стоимость связи
1	0,434	7,77
2	0,491	5,26
3	0,522	4,54
4	0,557	4,50
5	0,589	4,48
8	0,691	4,45
10	0,767	4,45
15	0.985	4,45
20	1,240	4,45
25	1,503	4,45
30	1,767	4,45
39	2,245	4,45

2.2.6 Алгоритм D-структур

В модели многопунктовой ЛС, используемой как в унифицированном алгоритме Кершенбаума — Чжоу, так и в алгоритмах Исау — Вильямса, Мартина, Краскала и других, учитывают следующее допущение: при подключении очередного АП к многопунктовой сети стоимость канала передачи данных между узлами iи j не зависит от объема информации hi, при этом вводится лишь одно ограничение: fij≤ d, где fij— суммарный поток (трафик) в любой ветви (i, j). Такое допущение справедливо в случае, когда по всей длине многопунктовой связи ее пропускная способность dостается постоянной. Вместе с тем использование модемов, работающих с различными скоростями передачи данных, позволяет организовать многопунктовые связи, в которых пропускная способность постепенно изменяется по мере приближения линии к центру обработки данных.

Таким образом, для многопунктовых связей с изменяемой (регулируемой) пропускной способностью традиционно используемое допущение (hi) = const оказывается неверным, что исключает возможность использования унифицированного алгоритма Кершенбаума—Чжоу.

Для решения задачи синтеза структуры древовидной сети при переменной скорости передачи данных предложен алгоритм D-структур. Важной особенностью алгоритма D-структур является то, что на шаге 1 определяются оптимальные места размещения РЦ и радиальная структура СДО, а затем она преобразуется в древовидную структуру. Рассмотрим описание алгоритма. Введем следующие обозначения: Хi, Xj— подграфы графа X, Xi = {xi*, xi2, ... , Xin}; xi* — направляющая вершина подграфа Хiт. е. его концевая вершина на данной итерации, куда сходятся информационные потоки из всех хЄХi. Будем предполагать, что подключить Xiк Xjможно введением ветви (i*, j), исходящей только из направляющей вершины xi*, причем хjЄХj, и на Xjограничения не накладываются; Hi— суммарный объем ИВР подграфа Xi, ,hij— суммарный поток в ветви (i, j); С(Хi)— стоимость передачи информации во всех ветвях подграфа Xi.

1.Применяем алгоритм синтеза R-структур, находим размещение РЦ Y* = {yi*} и привязки абонентов к РЦ Хyi.Далее предполагаем, что РЦ размещен в пункте 1.

2.Определяем начальные веса всех вершин vi= (hi,li1) и выполняем переход на подпрограмму «Оценка» (шаги 3—20).

Подпрограмма «Оценка». В подпрограмме «Оценка» определяем стоимость передачи объема информации Hiот подграфа Xiк подграфу Xjпри наилучшем варианте подключения. Пусть к началу итерации построено К. подграфов X1, Х2 , … Хк.

3.Выбираем изолированный подграф Хi.

4.Проверяем возможность введения ветви (i, j)

Нi + Нj≤dmax

Если условие выполняется, то переходим к шагу 5, в противном случае полагаем, что экономия Еij = ∞, переходим к шагу 4 и выбираем другую пару подграфов Хr, Хlдля анализа.

5.Отыскиваем вершину xj1, (xj1 Є Хj), ближайшую к xi*:

6. Проверяем, является ли xj1направляющей в подграфе Xj. Если — да, то запоминаем дугу (i*, j*), вычисляем = Ci*j*(Hi,li*j*), Н’j=Нj + Нiи переходим к шагу 21, иначе — к шагу 7. Шаги 7—20 предназначены для нахождения наилучшего варианта подключения Хiк Xj.

7. Определяем направленный маршрут из xi* в xj* через вершину xj1. Пусть им окажется πi*j*={xi* – xj1 – xj2 – … xjk}, xjk=xj*.

8. Вычисляем Сi*j1 = (Hi,li*j1), находим ni*j1 = ]Hi/d[, где ni*j1 — число каналов в ветви (i*, j1); знаком] [ обозначено округление с избытком. Пусть nikjk — число каналов в ветви (ik, jк).

9. Принимаем Сij= 0; Сij = (li*j1).

10.Полагаем s = 0, где s — номер итерации.

11.s=s+1.

12.Проверяем условие, все ли ветви маршрута πi*j* просмотрены. Если s<K, то переходим к шагу 13, иначе — к 21.

13.Вычисляем (Hi) — приращение стоимости для передачи дополнительного объема информации Hi:

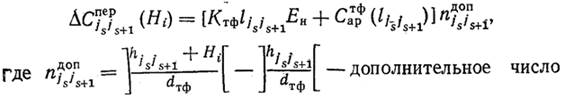
единичных каналов, которые необходимо установить в ветви (js, js+1); dТФ — ПС телефонного канала связи.