Реферат: Абсорбция 2
Если уА - мольная доля извлекаемого компонента А в газовой смеси и Р - общее давление в системе, то парциальное давление рА , по закону Дальтона, можно выразить зависимостью
![]() (4)
(4)
Подставив значение рА в уравнение (1), получим
 (5)
(5)
или закон Генри может быть представлен в форме
![]()
где т = E / P - коэффициент распределения, или константа фазового равновесия.
Уравнение (5) показывает, что зависимость между концентрациями данного компонента в газовой смеси и в равновесной с ней жидкости выражается прямой линией, проходящей через начало координат и имеющей угол наклона, тангенс которого равен т. Числовые значения величины т. зависят от температуры и давления в системе: уменьшаются с увеличением давления и снижением температуры. Таким образом, растворимость газа в жидкости увеличивается с повышением давления и снижением температуры.
Когда в равновесии с жидкостью находится смесь газов, закону Генри может следовать каждый из компонентов смеси в отдельности.
Закон Генри применим к растворам газов, критические температуры которых выше температуры раствора, и справедлив только для идеальных растворов. Поэтому он с достаточной точностью применим лишь к сильно разбавленным реальным растворам, приближающимся по свойствам к идеальным, т. е. соблюдается при малых концентрациях растворенного газа или при его малой растворимости. Для хорошо растворимых газов, при больших концентрациях их в растворе, растворимость меньше, чем следует из закона Генри. Для систем, не подчиняющихся этому закону, коэффициент т в уравнении (5) является величиной переменной и линия равновесия представляет собой кривую, которую строят обычно по опытным данным.
Для описания равновесия между газом и жидкостью уравнение (5) применимо только при умеренных давлениях, невысоких температурах и отсутствии химического взаимодействия между газом и поглотителем.
При повышенных давлениях (порядка десятков атмосфер и выше) равновесие между газом и жидкостью не следует закону Генри, так как изменение объема жидкости вследствие растворения в ней газа становится соизмеримым с изменением объема данного газа. При этих условиях константу фазового равновесия можно определить следующим образом:
 (6)
(6)
где f 0 - фугитивность (летучесть) поглощаемого газа, выраженная в единицах давления.
Для бинарных растворов величина f 0 может быть найдена следующим образом:
![]() (7)
(7)
где А – постоянная.
При выражении состава фаз не в абсолютных, а в относительных концентрациях видоизменяется и запись закона Генри. Так, например, при использовании относительных мольных концентраций выражение (5) можно записать в виде

откуда по правилу пропорций

Или
 (8)
(8)
Следовательно, при выражении закона Генри в относительных концентрациях равновесие в системе газ-жидкость изображается также кривой линией. Однако для сильно разбавленных растворов (малые концентрации X газа в жидкости) можно принять (1 - т) X ≈ 0. Тогда знаменатель уравнения (8) обращается в единицу и уравнение принимает вид
![]() (9)
(9)
При таком выражении закон Генри изображается прямой линией. Таким образом, уравнения (1), (2), (5), (8) и (9) являются различными выражениями закона Генри.
В случае абсорбции многокомпонентных смесей равновесные зависимости значительно сложнее, чем при абсорбции одного компонента, особенно тогда, когда раствор сильно отличается от идеального. При этом парциальное давление каждого компонента в газовой смеси зависит не только от его концентрации в растворе, но также и от концентрации в растворе остальных компонентов, т. е. является функцией большого числа переменных. Поэтому, как правило, в подобных случаях равновесные зависимости основываются на опытных данных.
Материальный баланс процесса абсорбции
Материальный баланс и расход абсорбента. Примем расходы фаз по высоте аппарата постоянными и выразим содержание поглощаемого газа в относительных мольных концентрациях. Обозначим: G - расход инертного газа, кмоль/сек; Y н и Y к - начальная и конечная концентрации абсорбтива в газовой смеси, кмоль/кмоль инертного газа; L - расход абсорбента, кмоль/сек; его концентрации Хн и Хк , кмоль/кмоль абсорбента. Тогда уравнение материального баланса будет:
![]() (10)
(10)
Отсюда общий расход абсорбента (в кмоль/сек )
![]() (11)
(11)
а его удельный расход (в кмоль/кмоль инертного газа)
![]() (12)
(12)
Это уравнение можно переписать так:
![]() (13)
(13)
Уравнение (13) показывает, что изменение концентрации в абсорбционном аппарате происходит прямолинейно и, следовательно, в координатах Y - X рабочая линия процесса абсорбции представляет собой прямую с углом наклона, тангенс которого равен ![]() .
.
Между удельным расходом абсорбента и размерами аппарата существует определенная связь. Через точку В с координатами Хн и Y к (рисунок 3) проведем, согласно уравнению (13), рабочие линии ВА, ВА1 , ВА2 , ВА3 , отвечающие различным концентрациям абсорбента или разным удельным его расходам. При этом точки А, А1 , А2 , А3 будут лежать на одной горизонтальной прямой в соответствии с заданной начальной концентрацией Y н газа в смеси.
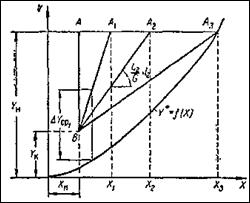
Рисунок 3 - К определению удельного расхода абсорбента
В случае растворов небольшой концентрации для любого значения Х и выбранной величины l движущая сила процесса выражается разность ординат Y - Y * , изображенных вертикальными отрезками, соединяющими соответствующие точки рабочей линии и линии равновесия Y * = f ( X ). Для всего аппарата можно принять среднее значение ∆ Y ср , величин: которого, например для рабочей линии BA 1 изображена на рисунке отрезком ∆ Y ср 1 . Величина ∆ Y ср будет тем больше, чем круче наклон рабочих линий и, следовательно, чем больше удельный расход абсорбента. Если рабочая линия ВА совпадает с вертикалью, то движущая сила процесса имеет максимальное значение, однако удельный расход абсорбента l при этом будет бесконечно большим (так как Хк = Хн ). Если же линия рабочих концентраций ВА3 касается линии равновесия, то удельный расход абсорбента минимален (l = lmin ), а движущая сила в точке касания равна нулю, поскольку в этой точке рабочая концентрация равна равновесной. В первом случае размеры абсорбционного аппарата будут наименьшими при бесконечно большом расходе абсорбента, во втором - расход абсорбента наименьший при бесконечно больших размерах аппарата. Таким образом, оба случая являются предельными и практически неосуществимы.