Реферат: Алгоритми розрахунку періодичного режиму в нелінійній схемі
В даний час в алгоритмах чисельного інтегрування проблемно-орієнтованих програм використовується кінцево-різницеві методи, які мають бажану стійкість та дозволяють оцінювати локальну методичну похибку на кожному кроці. За допомогою цієї оцінки підтримується максимальний розмір кроку і вибирається мінімальний порядок методу. Для зменшення об’єму розрахунків в неявних методах ![]() розраховується спочатку за відповідною явною формулою (прогноз), а потім уточнюється за допомогою неявної (корекція). Після вибору методу чисельного інтегрування програміст основні зусилля направляє на створення ефективного алгоритму, який визначає розмір кроку.
розраховується спочатку за відповідною явною формулою (прогноз), а потім уточнюється за допомогою неявної (корекція). Після вибору методу чисельного інтегрування програміст основні зусилля направляє на створення ефективного алгоритму, який визначає розмір кроку.
Відносно методів інтегрування, спираючись на розклад невідомої функції в ряд Тейлора, наприклад методом Рунге-Кутта різних порядків, можна зазначити, що вони знаходять обмежене використання. Пов’язано це з двома обставинами: по-перше, ускладнюється оцінка локальної методичної похибки на кожному кроці інтегрування; по-друге, для визначення ![]() треба m разів обчислити значення першої частини диференційних рівнянь (m – порядок методу), причому ці значення неможливо використовувати на інших кроках. Друга властивість знижує ефективність розрахунків порівняно з кінцево-різницевими формулами. Методом Рунге-Кутта зручно починати чисельне інтегрування, якщо воно ведеться за багатокроковими різницевими формулами, для отримання необхідних початкових значень. Справа в тому, що методи Рунге-Кутта виявляються явними та однокроковими. Тому використання їх на початковій стадії обчислення не дуже позначиться на загальних часових втратах, а необхідна точність забезпечується правильним вибором порядку.
треба m разів обчислити значення першої частини диференційних рівнянь (m – порядок методу), причому ці значення неможливо використовувати на інших кроках. Друга властивість знижує ефективність розрахунків порівняно з кінцево-різницевими формулами. Методом Рунге-Кутта зручно починати чисельне інтегрування, якщо воно ведеться за багатокроковими різницевими формулами, для отримання необхідних початкових значень. Справа в тому, що методи Рунге-Кутта виявляються явними та однокроковими. Тому використання їх на початковій стадії обчислення не дуже позначиться на загальних часових втратах, а необхідна точність забезпечується правильним вибором порядку.
3. Спектральні методи
1 Математичний зміст спектральних методів. Розглянемо розрахунок періодичного режиму в нелінійному пристрої на прикладі конкретної схеми (рис. 1), складеної з паралельно з’єднаних провідностей y(p), нелінійного опору з вольт-амперною характеристикою ![]() та нелінійної ємності, в якій відома вольт-кулонівська характеристика
та нелінійної ємності, в якій відома вольт-кулонівська характеристика ![]() . Аргументом лінійної провідності є оператор диференціювання
. Аргументом лінійної провідності є оператор диференціювання ![]() .
.
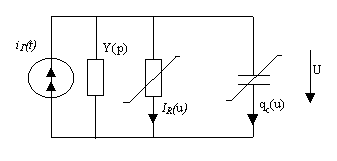
Рисунок 1 – Схема, за допомогою якої ведеться розрахунок періодичного режиму
На вході схеми діє періодичне джерело струму із періодом ![]()
![]() . ( 2)
. ( 2)
При заданих y(p), ![]() ,
, ![]() ,
, ![]() потрібно знайти періодичну з періодом
потрібно знайти періодичну з періодом ![]() напругу
напругу ![]() , яка буде рішенням диференційного рівняння, записаного в символічній формі
, яка буде рішенням диференційного рівняння, записаного в символічній формі
![]() .
.
Подамо шукану напругу в формі ряду Фур’є:
![]() . (3)
. (3)
Задача зводиться до визначення спектральних компонентів в (3).
Очевидно, при періодичному режимі струм нелінійного опору та заряд нелінійної ємності будуть також періодичними функціями часу
![]() , (4)
, (4)
![]() . (5)
. (5)
Важливо мати на увазі, що кожна амплітуда струму та заряду в (4) і (5) буде, в силу (3), функцією всіх комплексних амплітуд шуканої напруги.
Щоб отримати рівняння для ![]() , підставимо (3), (4) та (5) в диференційне рівняння
, підставимо (3), (4) та (5) в диференційне рівняння
![]() .
.
Тут усі комплексні амплітуди постійні. Значить, оператор диференціювання діє тільки на експоненційні функції
![]() ;
; ![]() .
.
Отже, можна записати
![]() ,
,
де ![]() ={1 при k=0, ±1; 0 при k
={1 при k=0, ±1; 0 при k![]() 0, ±1}.
0, ±1}.
Отримане співвідношення являє собою лінійну комбінацію функцій ![]() . Оскільки вони лінійно незалежні, то складена лінійна комбінація може обернутись в нуль тільки при рівності нулю кожного співмножника в квадратних дужках:
. Оскільки вони лінійно незалежні, то складена лінійна комбінація може обернутись в нуль тільки при рівності нулю кожного співмножника в квадратних дужках:
![]() , (6)
, (6)
![]()
Вище зазначалось, що кожна амплітуда струму та заряду є функцією комплексних амплітуд напруги
![]() , (7)
, (7)