Реферат: Алгоритми розрахунку періодичного режиму в нелінійній схемі

Тому (6) являє собою нескінчену систему трансцендентних (нелінійних) рівнянь відносно комплексних амплітуд напруг.

При практичних розрахунках досить врахувати постійну складову і кілька гармонік напруги. Так можна зробити тому, що розглянуті схеми вибірні. Звичайно, кількість гармонік, які беруться до уваги, повинен визначити розробник. Зазначимо, що в інженерній методиці розрахунку подібних схем, враховується лише одна гармоніка.

Допустимо, встановлено, що досить полічити N гармонік. Тобто, система (6) складається з (2 N + 1) рівнянь. Таким чином, розрахунок періодичного режиму спектральним методом зводиться до рішення системи нелінійних рівнянь. Різновиди методу визначаються способом рішення цієї системи.

Потрібно взяти до уваги особливість рівнянь (6): в них нелінійні функції (7) в деяких випадках можна описати аналітично. У зв’язку з цим, далі не розглядатимемо способи рішення (6), які спираються на аналітичне уявлення функції (7). Тому нижче зупинимося на двох способах: перший – ітераційний метод Ньютона; другий – різновид пропонованого у методу, що спирається на інтегрування диференційних рівнянь.

2 Алгоритм рішення системи нелінійних рівнянь методом Ньютона.

Запишемо рівняння (17) у векторно-матричній формі

, (8)

де - вектор комплексних амплітуд струму комплексних амплітуд напруги;

- вектор нелінійного опору;

- вектор комплексних амплітуд заряду нелінійної ємності;

- вектор складової джерела струму;

та - квадратні діагональні матриці. Розмірність векторів та матриць дорівнює 2N+1.

Ліва частина формули (7), виявляється трансцендентною векторною функцією, аргумент якої – вектор напруги

. (9)

За допомогою формули (7) отримаємо співвідношення для методу Ньютона стосовно (9)

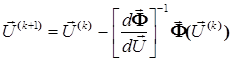. (10)

Верхній індекс вектора напруги вказує на номер ітерації.

Якщо в (9) підставити , то в лівій частині не отримаємо нуль. Тому вектор – функцію називають незв’язною.

Продиференцюємо (10) по вектору

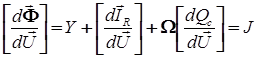. (11)

Нагадаємо, що похідна від вектор-функції незв’язності за векторним аргументом виявляється матрицею Якобі. Як видно, вона складається з трьох складових. Позначимо і елементи матриць та .Тоді

, , .

В даному випадку використання методу Ньютона особливо ефективне, оскільки вдається отримати аналітичний вираз для і . Покажемо, як знаходиться, наприклад, .

За визначенням

.

Величину запишемо у вигляді

.

В свою чергу ,

.