Реферат: Анализ и моделирование биполярных транзисторов

Соответственно для имеем

Токи коллектора и эмиттера с учетом (10.2) примут вид

(10.3)

На основании закона Кирхгофа ток базы

(10.4)

При использовании (10.1)-(10.4) следует помнить, что в полупроводниковых транзисторах в самом общем случае справедливо равенство

(10.5)

Решив уравнения (10.3) относительно , получим

(10.6)

Это уравнение описывает выходные характеристики тран­зистора.

Уравнения (10.3), решенные относительно , дают выраже­ние, характеризующее идеализированные входные характеристи­ки транзистора:

(10.7)

В реальном транзисторе кроме тепловых токов через переходы протекают токи генерации — рекомбинации, каналь­ные токи и токи утечки. Поэтому ,, , как правило, неизвестны. В технических условиях на транзисторы обычно приводят значения обратных токов p-n-переходов ,. определенные как ток соответствующего перехода при неподключенном выводе другого перехода.

Если p-n-переход смещен в обратном направлении, то вместо теплового тока можно подставлять значение обратного тока, т. е. считать, что и . В первом приближении это можно делать и при прямом смещении p-n-перехода. При этом для кремниевых транзисторов вместо следует подставлять , где коэффициент m учитывает влияние токов реального перехода (m = 2 - 4). С учетом этого уравнения (10.3), (10.5) часто записывают в другом виде, который более удобен для расчета цепей с реальными транзисторами:

(10.8)

(10.9)

(10.10)

где .

Различают три основных режима работы биполярного транзистора: активный, отсечки, насыщения.

В активном режиме один из переходов биполярного тран­зистора смещен в прямом направлении приложенным к нему внешним напряжением, а другой - в обратном направлении. Соответственно в нормальном активном режиме в прямом направлении смещен эмиттерный переход, и в (10.3), (10.8) напряжение имеет знак «+». Коллекторный переход смещен в обратном направлении, и напряжение в (10.3) имеет знак « - ». При инверсном включении в уравнения (10.3), (10.8) следует подставлять противоположные полярности напряжений , . При этом различия между инверсным и активным режимами носят только количественный характер.

Для активного режима, когда и (10.6) запишем в виде .

Учитывая, что обычно и , урав­нение (10.7) можно упростить:

(10.11)

Таким образом, в идеализированном транзисторе ток коллектора и напряжение эмиттер-база при определенном значении тока не зависят от напряжения, приложенного к коллекторному переходу. В действительности изменение напряжения меняет ширину базы из-за изменения размеров коллекторного перехода и соответственно изменяет градиент концентрации неосновных носителей заряда. Так, с увеличением ширина базы уменьшается, градиент концентрации дырок в базе и ток увеличиваются. Кроме этого, уменьшается вероятность рекомбинации дырок и увеличивается коэффициент . Для учета этого эффекта, который наиболее сильно проявляется при работе в активном режиме, в выражение (10.11) добавляют дополнительное слагаемое

(10.12)

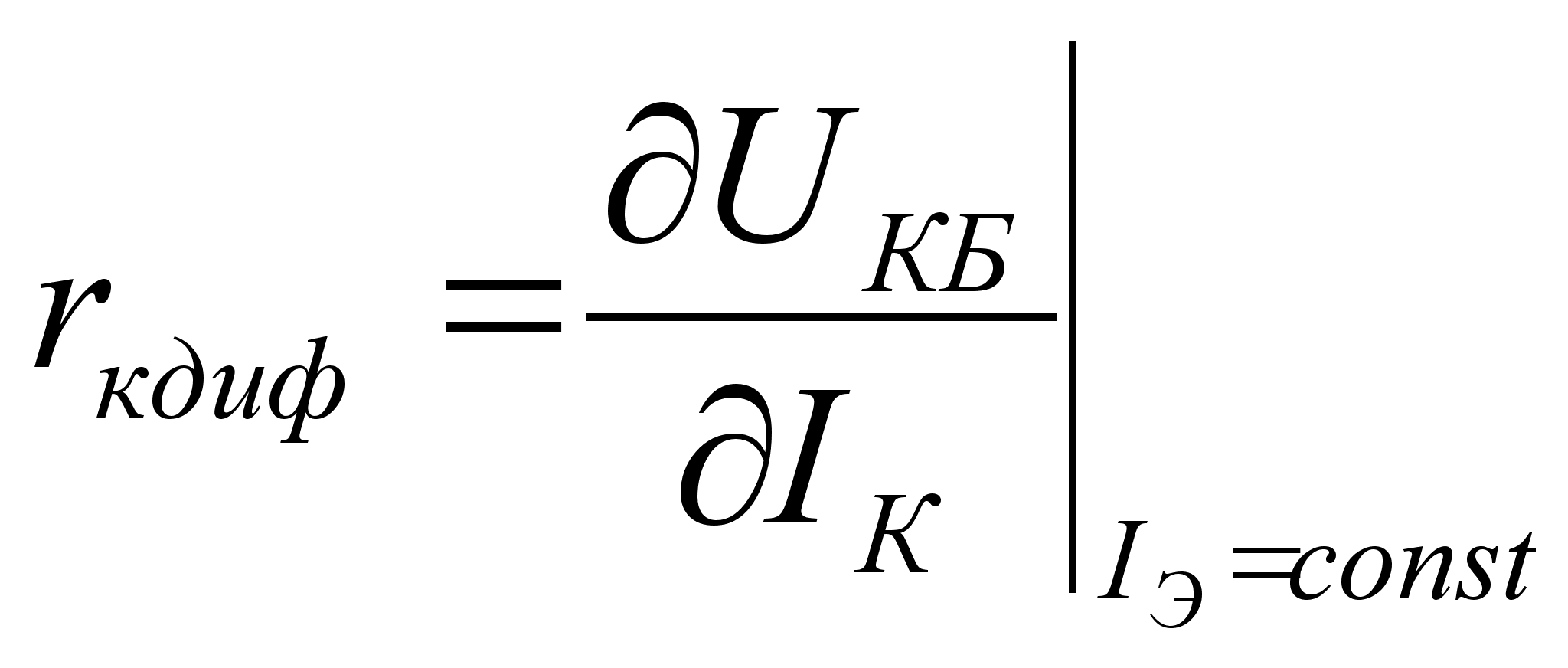- дифференциальное сопротивление запертого коллекторного p-n-перехода.

Влияние напряжения на ток оценивается с помощью коэффициента обратной связи по напряжению

,
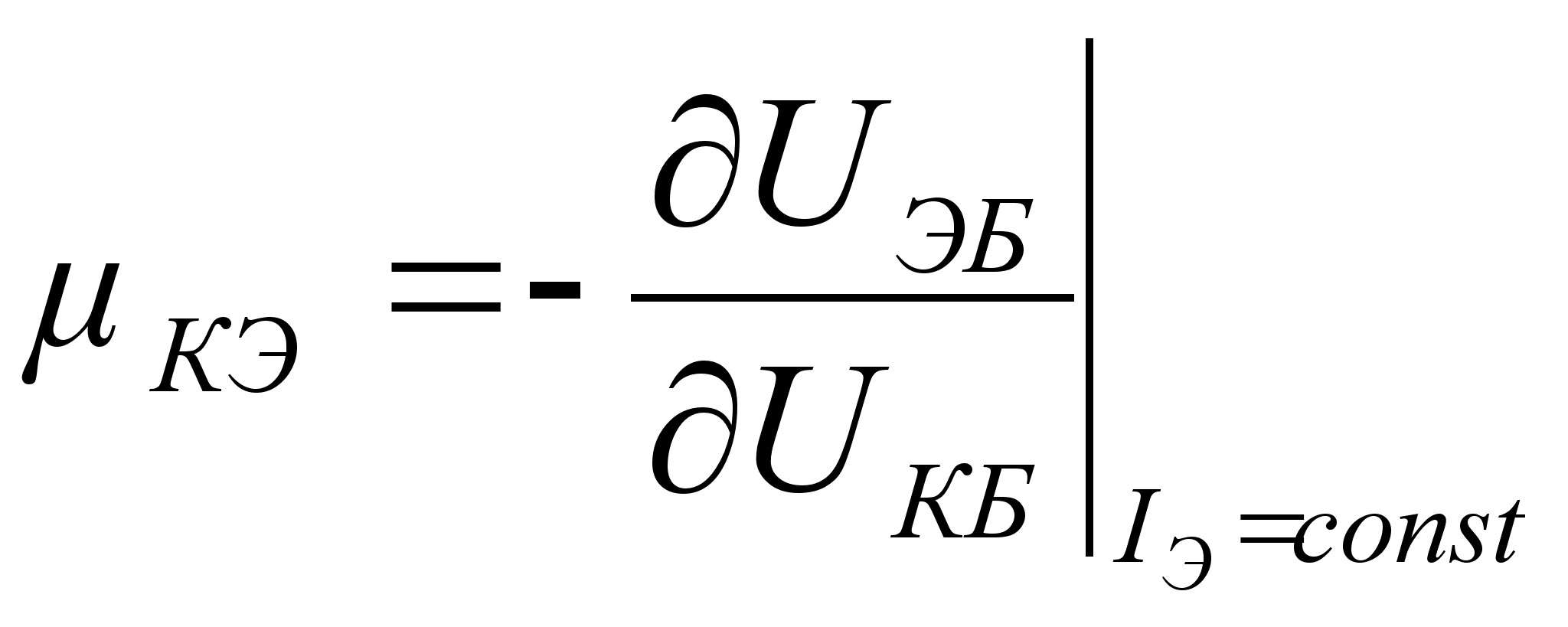