Реферат: Анализ криптостойкости методов защиты информации в операционных системах Microsoft Window 9x

На следующем шаге, получив линейные аппроксимации, в матричной форме записывают базовые уравнения комбинирующего узла с памятью

S_t+1 = AS_t + BX_t + (X_t, S_t), t≥0,

y_t = CS_t + DX_t + (X_t, S_t), t ≥0,

где векторы рассматриваются как матрицы-столбцы; A, B, C, D - двоичные матрицы; а  и каждый компонент в D = (d₁, . . . , d_M) – несбалансированные булевы функции, именуемые функциями шума. Основная идея состоит в том, чтобы рассматривать {(X_t ,S_t)}_t=0^ и {(X_t ,S_t)}_t=0^ , 1≤i≤M, в качестве входных последовательностей, так что последние уравнения оказываются задающими неавтономную линейную машину с конечным числом состояний или ЛПС, именуемую АЛПС комбинирующего узла с памятью. Тогда можно решать эту ЛПС с использованием техники производящих функций (D-преобразований). В частности, пусть S, X, , , y обозначают производящие функции от переменной z для последовательностей {S_t}, {X_t}, (X_t, S_t)},  (X_t, S_t)}, y_t}, соответств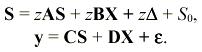
енно. Тогда уравнения сводятся к виду

Р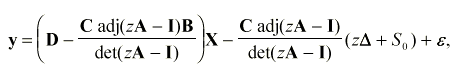
ешение имеет вид

где I - единичная матрица, det(zA - I) = (z), (0) = 1, - многочлен, обратный к характеристическому многочлену матрицы переходов A степени, не превышающей ранг A (≤M); а элементы (присоединенной) матрицы adj(zA - I) - это полиномы от z степени не более M-1. Вычислительная сложность для отыскания такого решения составляет O(M³(N+1)). В другом виде решение можно переписать как

г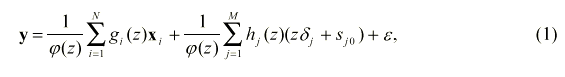

де x_i и _j обозначают производящие функции для {x_it} и {_j(X_t, S_t)}, а степени полиномов g_i(z) и h_j(z) самое большее равны M и M-1, 1≤i≤N, 1≤j≤M, соответственно. Полагая

решение можно преобразовать к виду:

г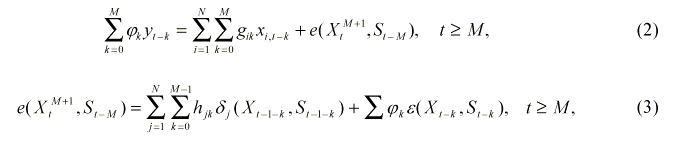
де подразумевается, что вектор состояния S_t-k - это функция от (X_t-k-1^M-k, S _t-M) для каждого 0≤k≤M-1. Линейные функции входа и выхода в (2) скоррелированы тогда и только тогда, когда функция шума e несбалансирована. Коэффициент корреляции не зависит от времени, если функция следующего состояния сбалансирована. Если это условие не удовлетворяется, то корреляционный коэффициент может зависеть от времени, поскольку от S_t более не требуется сбалансированность для каждого t≥0. Функция шума e в (3) определена как сумма индивидуальных шумовых функций, которые несбалансированы при условии, что сбалансирована функция следующего состояния. Поскольку от индивидуальных шумовых функций не требуется быть независимыми, в принципе нельзя исключать возможность, что коэффициент корреляции e с константной нулевой функцией равен нулю или очень близок к этому значению.

В рассматриваемом случае индивидуальные шумовые функции можно трактовать как булевы функции от n = MN + N + M переменных в (X^M+1_t , S_{t -M}). Следовательно, за исключением некоторых особых случаев, в общем случае можно с высокой вероятностью ожидать, что общий корреляционный коэффициент очень близок к произведению индивидуальных и, таким образом, отличается от нуля. Соответственно, метод АПЛС не только с высокой вероятностью дает взаимно коррелированные линейные функции от входа и выхода, но также позволяет оценить значение соответствующего корреляционного коэффициента, используя независимость или другие вероятностные предположения. Поскольку в идеальном случае хотелось бы получить такие АЛПС, в которых корреляционные коэффициенты по абсолютному значению близки к максимуму, то индивидуальные корреляционные коэффициенты должны быть крупными по величине, а количество шумовых членов в (3) должно быть маленьким. Конечно, эти требования могут противоречить друг другу. Поэтому хорошим подходом будет повторение процедуры АЛПС несколько раз, начиная с наилучших линейных аппроксимаций для функции выхода и компонент функции следующего состояния. Эта процедура может также выполняться для всех возможных линейных аппроксимаций, что представляется единственным систематическим способом проверить все корреляции, выявленные в процессе применения метода АЛПС. В общем случае имеется самое большее (M+1)2^M+N таких линейных аппроксимаций. Однако, в принципе всегда можно проверить все возможные линейные аппроксимации даже при большом M, поскольку в практических реализациях функции выхода и следующего состояния зависят от сравнительно небольшого количества переменных или же составлены из таких булевых функций.

С практической точки зрения данная линейная модель может быть использована для выделения по шифротексту генератора RC4 среди других криптосистем, а также для восстановления параметра n. В 2000 году была опубликована статья Скотта Флюера и Дэвида Мак-Гри посвященная статистистическому анализу потокового генератора RC4, в которой были использованы результаты работы Голича для нахождения значения компонент S-бокса. Приблизительное время работы этого метода составляет 2⁶ⁿ, где n – порция битов в выходном потоке, длина выходной последовательности, требуемая для выявления статистической слабости, близка к 2³⁰. Полученный результат указывает на существенную слабость генератора и возможность восстановить параметры i и n. S-бокс может принимать 2^nk, где n_k – число битов ключа.

2. Защита информации в операционных системах Microsoft Windows 9x

2.1 Аутентификация, безопасность и доступ к ресурсам в операционных системах семейства Microsoft Windows 9x

В операционных системах Microsoft Windows 9x для аутентификации пользователя используется имя пользователя, а для подтверждения введенного имени – процедура аутентификации, использующая символьный пароль пользователя. Алгоритм этой процедуры, которая вызывается из библиотеки MSPWL32.DLL, состоит из следующих шагов:

Шаг 1. Пользователь вводит свое имя и пароль в формате Unicode.

Шаг 2. Имя и пароль преобразуется в формат ASCII, причем строчные буквы преобразуются в прописные.

Шаг 3. Осу?