Реферат: Анализ Монополий
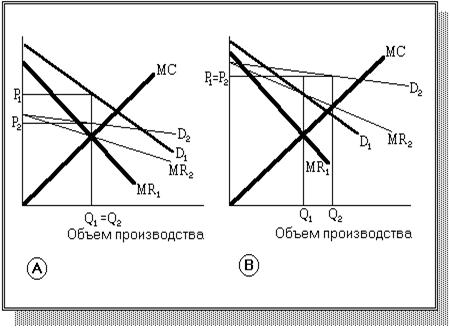
Как мы можем проверить, что Q* - объем производства, максимизирующий прибыль? Предположим, монополист производит меньшее количество продукции - Q1 и соответственно получает более высокую цену Р1 . Как показывает рис.1, в таком случае предельный доход монополиста превышает предельные издержки, и если бы он производил большее количество продукции, чем Q1 , он получил бы добавочную прибыль (МR - МС), т.е. увеличил бы свою совокупную прибыль. Фактически монополист может увеличивать объем производства, повышая свою совокупную прибыль вплоть до объема производства Q* , при котором дополнительная прибыль, получаемая от выпуска еще одной единицы продукции, равна нулю. Поэтому меньшее количество продукции Q1 не максимизирует прибыль, хотя и позволяет монополисту установить более высокую цену. При объеме производства Q1 вместо Q* совокупная прибыль монополиста будет меньше на величину, равную заштрихованной площади между кривой МR и кривой МС, между Q1 и Q* .
На рис.1 больший объем производства Q2 также не является максимизирующим прибыль. При данном объеме предельные издержки превышают предельный доход, и если бы монополист производил меньшее количество, чем Q2, он увеличил бы совокупную прибыль (на МС - МR). Монополист мог бы увеличить прибыль еще больше, сокращая объем производства до Q* . Увеличение прибыли за счет снижения объема производства Q* вместо Q2 дано площадью ниже кривой МС и выше кривой МR, между Q* и Q2 . Мы также можем показать алгебраически, что объем производства Q* максимизирует прибыль. Прибыль равна разности между доходом и издержками, которые представляют собой функцию от Q:
p(Q) = TR(Q) - TC(Q).
По мере того как Q растет, начиная с нуля, прибыль будет возрастать до тех пор, пока не достигнет максимума, а затем станет снижаться. Таким образом, объем производства Q максимизирует прибыль в том случае, когда приращение прибыли от дополнительного увеличения Q равно нулю (т.е. Dp/DQ = 0). Тогда
![]()
Но DTR/DQ является предельным доходом, а DC/DQ - предельными издержками, и поэтому условием максимизации прибыли является
MR - MC = 0 или MR = MC.
1.2. Правило "большого пальца" для ценообразования
Мы знаем, что цена и объем производства должны быть такими, чтобы предельный доход равнялся предельным издержкам, но как может практически руководитель фирмы правильно определить соответствующие цену и объем производства? Большинство руководителей располагают ограниченной информацией о кривых средних и предельных доходов, с которыми сталкиваются их фирмы. Они также располагают информацией о предельных издержках фирмы лишь для изменяющихся в определенных пределах объемов производства. Мы, следовательно, хотим перевести условие равенства предельного дохода и предельных издержек в универсальное правило, которым легче пользоваться на практике.
Чтобы сделать это, мы должны переписать формулу предельного дохода следующим образом:
MR = DTR/DQ =D(PQ)/DQ.
Отметим, что дополнительный доход, получаемый в результате выпуска дополнительной единицы продукции, D(PQ)/DQ обладает двумя свойствами. Произведя одну дополнительную единицу продукции и продавая ее по цене Р, мы получим доход: (1)•(Р) = Р. Но фирма сталкивается с кривой спроса, имеющей наклон вниз, и поэтому производство и продажа данной дополнительной единицы приводят к небольшому снижению в цене DP/DQ, которое уменьшает доход от всей проданной продукции (т.е. изменение дохода Q[DP/DQ]).
Таким образом:
![]()
Правую часть формулы мы получили, умножив выражение Q (DP/DQ) на Р, а затем разделив его на Р. Вспомним, что эластичность спроса выражается как Еd =(P/Q)•(DQ/DP). Таким образом, (Q/P)•(DP/DQ) есть выражение, обратное эластичности спроса 1/Еd следовательно, при объеме производства, максимизирующем прибыль, можно записать:
![]()
Теперь, так как целью фирмы является максимизация прибыли, мы можем приравнять предельный доход к предельным издержкам:
P + P (1/Ed ) = MC,
или,
![]() (1)
(1)
Данная формула представляет собой правило "большого пальца" для ценообразования. Левая часть уравнения (P - MC)/P выражает превышение цены над предельными издержками как процент от цены. Уравнение показывает, что данное превышение равняется величине, обратной эластичности спроса, взятой с отрицательным знаком. Точно так же мы можем переписать это уравнение, чтобы выразить цену через предельные издержки:
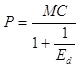 (2)
(2)
Например, если эластичность спроса равняется -4, а предельные издержки 9 долл. на единицу продукции, цена должна составить: 9/(1 - 1/4) = 9/0,75 = 12 долл. за единицу.
Как сравнить цену, устанавливаемую монополистом, с ценой в условиях свободной конкуренции? На совершенном конкурентном рынке цена равна предельным издержкам. Монополист назначает цену, превышающую предельные издержки на величину, обратно пропорциональную эластичности спроса. Как показывает уравнение (1), если спрос чрезвычайно эластичен, Еd представляет собой большую отрицательную величину, а цена будет близка к предельным издержкам и, таким образом, монополизированный рынок будет очень похож на рынок свободной конкуренции. Фактически, когда спрос очень эластичен, монополисту достается незначительная прибыль.
1.3. Смещение спроса
На конкурентном рынке существует прямая зависимость между ценой и объемом предложения. Эта зависимость отражена кривой предложения, которая совпадает с кривой издержек производства для отраслей в целом. Кривая предложения показывает, сколько будет производиться продукции по каждой цене.
|
К-во Просмотров: 806
Бесплатно скачать Реферат: Анализ Монополий
|