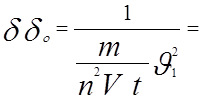Реферат: Анализ природы и свойств гравитационных волн методом электромеханической аналогии
Предположим, что в природе существуют некие заряды qx , которые создают Х-поле.
Также предположим, что любое тело способно накапливать эти заряды (qx ), то есть обладать Х-ёмкостью, тогда по аналогии, глядя на выражение электроёмкости 9), можно попытаться получить формулу для Х-ёмкости.
Так как формула 5) отличается от формулы 4) дополнительным множителем t и появлением вместо линейных размеров объёмных, то можем предположить, что Х-ёмкость отличается от электроёмкости 9) теми же параметрами:
10)- Х-ёмкость тела шарообразной формы (с точностью до некоторого, возможно численного коэффициента, не имеющего размерность), где
V- объём тела шарообразной формы,
t- промежуток времени в той системе, где измеряется масса тела шарообразной формы,
δ- иксовая проницаемость среды (вещества, тела),
δ0 - иксовая постоянная,
δδ0 - абсолютная иксовая проницаемость среды.
По аналогии с распространением электромагнитных волн скорость иксовых волн в среде:
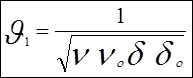11)
Допустив, что для вакуума
ν=1- (гравитационная проницаемость в вакууме)
δ=1-(иксовая проницаемость среды), можем предположить, что
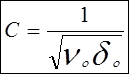12)- скорость света в вакууме, то есть скорость гравитационно-иксовых волн в вакууме равна скорости света (скорости электромагнитных волн в вакууме).
Примечание:
1) Наличие в формуле 10) 
множителя t считаем правомерным, так как думаем, что если масса тела зависит от течения (хода) времени, то и Х-ёмкость должна тоже зависеть от течения (хода) времени t, так как эти свойства тел обусловлены наличием единого гравитационного иксового процесса.
2) Наличие в формуле 10) множителя V считаем тоже правомерным, так как тело состоит из отдельных объёмных областей, а каждая область способна накапливать qx заряды, и эти области распределены по всему объёму V тела шарообразной формы.
Теперь попытаемся выразить иксовую ёмкость тела через массу этого тела, воспользовавшись формулами
5) 
и
11) 
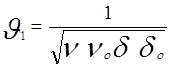, где m- масса тела шарообразной формы.
Из формулы 5) следует:
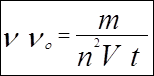
13)- абсолютная
гравитационная проницаемость среды.
Из формулы 11) следует:
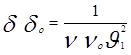
(учитывая формулу 13)
