Реферат: Анализ тестопригодности по методу Сamelot

Рисунок 5
Наличие ветвления на выходе устройства позволяет наблюдать его состояние на некоторых первичных выходах схемы. (Пвых1 и Пвых2).
OY(составное)=1-П [1-OY(каждого X-Пвых)],
OY(X-(Пвых1,Пвых2))=1-([1-OY(X-Пвых1)]*[1-OY(X-Пвых2)]).
4. Сходящиеся ветвления

Рисунок 6
1) Для путей неравной длины стратегия следующая: выбирается кратчайший путь и для него подсчитывается OY узла X, т.е. OY(X-Пвых). Предполагается, что на практике для активизации выбирается кратчайший путь, а другие блокируются во избежание возможности схождения информации.
2) Для сходящихся путей равной длины стратегия заключается в вычислении OY(X-Пвых) для обоих путей и выборе пути с наибольшим значением наблюдаемости. И вновь предполагается, что все остальные пути, кроме одного выбранного, могут быть блокированы.
5. Определение тестопригодности
Простая мера тестопригодности узла TY (testability) может быть получена умножением значения его CY и OY.
TY узла=CY узла * OY узла
На уровне интуитивного восприятия, если, скажем, СY=OY=0.5, то TY¹0.5, потому что если управлять узлом "на 50% сложнее" и наблюдать за узлом "на 50% сложнее", то в целом тестопригодность должна быть меньше 50%.
TY схемы = (STY узлов) / число узлов
Значения CY, OY, TY в чистом виде не используются, а используется ![]() от этих значений. Это позволяет ограничить масштаб абсолютных значений и облегчить интерпретацию результатов. Затем строятся гистограммы для CY, OY, TY. На оси абсцисс откладываются значения CY(OY, TY) от 0.1 до 1, на оси ординат - число узлов от 0 до n.
от этих значений. Это позволяет ограничить масштаб абсолютных значений и облегчить интерпретацию результатов. Затем строятся гистограммы для CY, OY, TY. На оси абсцисс откладываются значения CY(OY, TY) от 0.1 до 1, на оси ординат - число узлов от 0 до n.
Пример: Дан ![]() триггер. Подсчитать CY, OY, TY для узлов схемы и TY схемы.
триггер. Подсчитать CY, OY, TY для узлов схемы и TY схемы.
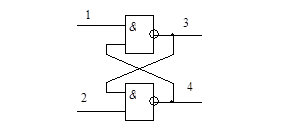
Рисунок 7
6. Определение управляемости
![]()
CY(1)=1
CY(2)=1
CY(3)=0.5*(CY(4)+1)/2
CY(4)=0.5*(CY(3)+1)/2
Решая систему линейных уравнений, имеем:
CY(3)=0.33
CY(4)=0.33
II Определение наблюдаемости