Реферат: Аналого-цифровое преобразование звуковых и видеосигналов

Введение

Среди методов цифрового представления ЗС наиболее известна импульсно-кодовая модуляция (ИКМ). Процедура преобразования аналогового сигнала в цифровой состоит из трех операций: дискретизации по времени, квантовании полученной совокупности отсчетов и замене квантованных значений сигнала последовательностью чисел (кодировании).

1. Дискретизация

Значение частоты дискретизации ограничивает разрешающую способность аналого-цифрового преобразования во времени и, следовательно, наивысшую возможную частоту на входе АЦП. Наглядной иллюстрацией этого служит рис. 1. Процедура дискретизации с одной и той же частотой f д представлена на рисунке одновременно для двух тональных сигналов низкой (F1 – сплошная линия) и высокой (F2 – штриховая линия) частот. В обоих случаях после дискретизации имеем идентичные временные последовательности значений отсчетов. Следовательно, сигналы этих двух частот F1 и F2 нельзя различить и после обратного преобразования правильно восстановить (реконструировать).

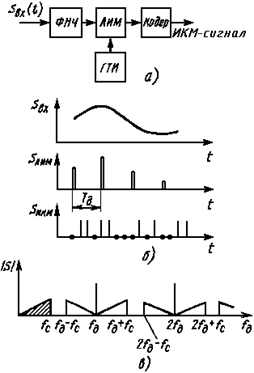
Рис. 1 Устройство, осуществляющее ИКМ (а), временная диаграмма процесса ИКМ (б), спектр дискретизированного сигнала (в)

В соответствии с теоремой отсчетов В.А. Котельникова неискаженная передача непрерывного (аналогового) сигнала с полосой частот 0…Fтах дискретной последовательностью его отсчетов возможна только в том случае, если частота f д связана с максимальной частотой Fmах исходного сигнала соотношением f д 2 Fтах .

Итак, если требуется передать синусоидальное колебание с частотой 20 кГц, то требуемая частота его дискретизации должна быть более 40 кГц, лишь в этом случае возможно точное восстановление непрерывного сигнала.

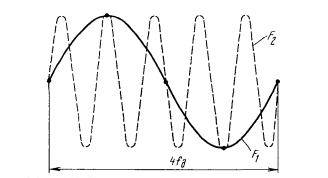
Рис. 2

Все сигналы, частота которых F >f д/2, при восстановлении интерпретируются неправильно и трансформируются в сигналы более низкой частоты.

Дискретизированный сигнал можно представить в следующих двух формах записи:

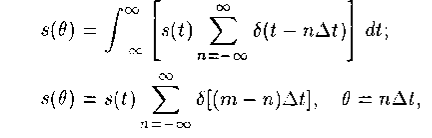
где s(t) – исходный аналоговый сигнал; Dt – интервал (период, шаг) дискретизации, причем Тд = D t = const; п = 0, 1, 2,…; d(t) – функция Дирака; d(т) – функция отсчетов, dп – моменты появления отсчетов ЗС.

При передаче ЗС или его обработке шаг дискретизации Тд не обязан быть одним и тем же в разных трактах канала или на разных стадиях обработки.

Рассмотрим теперь условия выбора частоты f д. Из рис. 2 следует, что чем больше f д по сравнению с Fтах, тем дальше в спектре дискретизированного сигнала разнесены частоты Fтах иf д и тем легче в ИКМ-демодуляторе отфильтровать полезный сигнал. В то же время скорость цифрового потока при ИКМ прямо пропорциональна значению f д. С точки зрения повышения эффективности канала связи при передаче сигналов 3В желательно насколько это возможно снизить f д. Однако выбор слишком низкого значения может привести к уменьшению допустимого значения Fтах и, как следствие, к ухудшению качества передачи. Поэтому значение f д выбирают исходя из компромисса между требуемым качеством звуковоспроизведения и допустимой скоростью цифрового потока. Влияют на выбор f д и системные факторы. Поскольку в системах связи сигналы 3В кодируются и передаются совместно с другими, например с телефонными сигналами, то частота дискретизации ЗС должна быть кратна частоте дискретизации телефонного сигнала. В противном случае в общей структуре цифрового потока системы связи невозможно обеспечить передачу более широкополосных сигналов 3В вместо нескольких телефонных. С учетом этих соображений при АЦП сигналов 3В в цифровых трактах первичного и вторичного распределений программ для ЗС с Fmах = 15 кГц принято значение f д = 32 кГц. что соответствует учетверенному значению f д для сигнала в телефонном канале.

В системах телевидения при передаче цифровых сигналов звукового сопровождения во избежание биений между гармониками строчной частоты и частоты дискретизации значение f д выбирается кратной частоте строчной развертки. В трактах формирования программ при Fmax = 20 кГц принято значение f д = 48 кГц, в лазерных проигрывателях и бытовых магнитофонах f д = 44,1 кГц.

Борьба с погрешностями цифрового преобразования из-за возможной нестабильности частоты дискретизации сводится к ограничению полосы частот ЗС фильтрами с полосой пропускания от 0 до Fmax на входе АЦП и выходе ЦАП и к выполнению требования теоремы В.А. Котельникова. Предъявляются жесткие требования к крутизне спада частотных характеристик ФНЧ за пределами полосы пропускания и стабильности частоты тактовых генераторов. Выполнение этих требований сегодня не вызывает трудностей.

2. Квантование

При квантовании непрерывному множеству мгновенных значений отсчетов аналогового сигнала ставят в соответствие конечное множество значений – уровней квантования. Иначе говоря, каждое значение отсчета заменяется ближайшим к нему разрешенным значением.

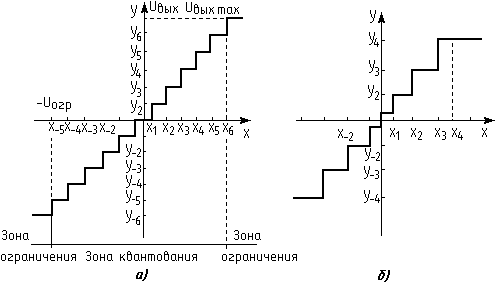
Расстояние между соседними разрешенными уровнями квантования называют шагом квантования. Процедуру квантования можно рассматривать как результат прохождения входного сигнала через устройство с амплитудной характеристикой ступенчатой формы (рис.), которая называется характеристикой (или шкалой) квантования. Если в пределах этой характеристики шаг квантования постоянен (Xi, – Xi-1 = D ═и Yi, – Yi-1 = D), то квантование называют равномерным (рис. 3). Этот простейший вид квантования широко используется в цифровой технике. Он удобен для начального цифрового представления ЗС с целью их последующей обработки, а также последующего сокращения избыточности цифровых сигналов при передаче их по каналам связи. Равномерное квантование часто служит также первым этапом для последующего неравномерного квантования.

Одним из наиболее важных показателей цифровых систем передачи аналоговых сигналов является величина отношения мощности сигнала Pс мощности шума квантования Ршкв на выходе ЦАП.

Определим значение Ршкв Для произвольной шкалы квантования.

Ршкв =1² /12

Отсюда следует важный вывод: при равномерном квантовании мощность шума квантования определяется исключительно шагом квантования и не зависит от величины сигнала. Поэтому при уменьшении уровня сигнала отношение мощности сигнала к мощности шума квантования снижается.

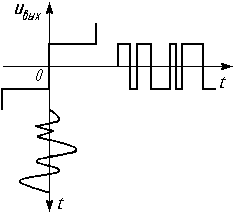
Рис. 3. Преобразование входных шумов в квантованное колебание в АЦП

Спектр шума квантования равномерный в полосе частот 0…f д/2. Шум квантования появляется только при наличии сигнала. При отсутствии сигнала на входе АЦП можно было бы ожидать, что на выходе ЦАП шум будет полностью подавлен. Однако наличие теплового шума входных аналоговых блоков АЦП, нестабильность напряжения питания, переходные помехи от соседних каналов, дрейф постоянной составляющей в усилителях постоянного тока и действие других факторов приводят к тому, что самый низкий первый уровень квантования достигается даже при отсутствии ЗС на входе АЦП.

На рис. 4 изображен начальный участок шкалы квантования и показано, как входные шумы преобразуются в АЦП в квантованное колебание. На выходе ЦАП это квантованное колебание превращается в шум, называемый шумом паузы. Шум паузы менее равномерный, чем белый шум, характерный для аналоговых систем. Его часто называют гранулированным. Мощность шума паузы Рш п⁼ 1 ² ═/4, т.е. на 4,7 дБ больше шума квантования.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--