Реферат: Аппроксимация характеристик нелинейных элементов и анализ цепей при гармонических воздействиях

(14)

Воспользовавшись известными формулами

(15)

представим равенство (14) так:

(16)

Отсюда вытекают следующие соотношения для расчета постоянной составляющей тока и амплитуд гармоник:

(17)

3. Анализ цепей методом угла отсечки

При работе нелинейной цепи с большими амплитудами входного сигнала, когда степенная аппроксимация не дает хороших результатов применяется кусочно-линейная аппроксимация. Работа НЭ происходит при этом с отсечкой выходного тока, и большое применение находит аналитический метод анализа, получивший название метода угла отсечки.

Форма тока в цепи, содержащей НЭ с характеристикой

(18)

видна из графика, представленного на рисунке 7 (при условии, что на вход подано напряжение ).

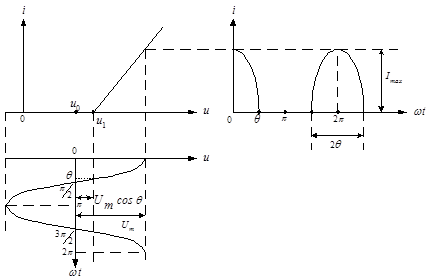
Рис. 7. График тока через НЭ при работе с отсечкой тока

График тока имеет характерный вид периодической последовательности косинусоидальных импульсов, которые характеризуются амплитудой и длительностью 2, где – угол отсечки, числено равный половине той части периода, в течение которого через НЭ протекает ток. Период повторения импульсов равен . Спектральный состав такого периодического колебания легко определить, разложив функцию тока в ряд Фурье:

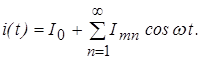(19)

Угол отсечки легко найти из равенства :

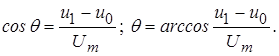(20)

Функция тока определяется следующим выражением:

. (21)

При :

. (22)

Амплитуды спектральных составляющих тока через НЭ определяются через коэффициенты Берга:

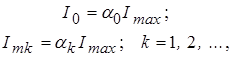(23)

где коэффициенты являются функциями одного аргумента – угла отсечки , получили название коэффициентов (функций) Берга.

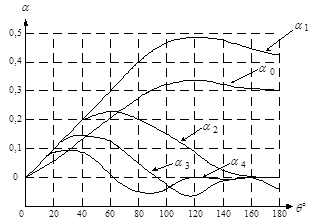
Рис. 8. Графики функций Берга

Анализ графиков функций позволяет сделать вывод о том, при каких углах отсечки амплитуды (n = 0, 1, 2, ...) имеют максимальные или минимальные (нулевые) значения. Это дает возможность с помощью выбора режима работы НЭ (изменяя напряжение смещения ,можно менять ) управлять соотношением амплитуд гармоник в спектре тока через НЭ.

Таким образом, алгоритм вычисления амплитуд гармоник тока через НЭ может быть следующим:

1. По известным значениям , , определяется угол отсечки с помощью формулы (18).