Реферат: АЦЭ - Разработка и расчёт автогенератора на диоде ганна с перестройкой частоты
Изм
Лист
№ докум
Подпись
Дата
|
Для получения зависимости m1 * и m2 * - эффективные массы k1 и k2 - подвижности n1 и n2 - концентрации электронов в нижней и верхней долинах соответственно. Из выражения для плотности тока в образце при Еп >Е
с учётом того, что n0 = n1 + n2 , получим
так как k1 >> k2 . Будем считать, что электронные температуры (Те ) в обеих долинах одинаковы. Тогда, исходя из статистики Максвелла - Больцмана, можно записать следующее выражение для отношения заселённостей электронами верхней и нижней долин:
где предэкспоненциальный множитель определяет отношение плотностей состояний в долинах, а М1 и М2 - число верхних и нижних долин соответственно. Для GaAS M 1 =1, M 2 =4, m1 * =0,067 m 0 , m2 * =0,55 m 0 и ( M 2/ M 1)(m2 * /m1 * )3/2 =94. Из (2) и (3) имеем
Выражение для Те получим, используя условие баланса энергии, приобретаемой электронами в электрическом поле в единицу времени и теряемой в это же время за счёт столкновений:
где Подстановка (4) в (5) приводит к следующему выражению
| ||||||
| Лист | ||||||
| 5 | ||||||
|
Изм | Лист | № докум | Подпись | Дата | ||
| Отсюда можно рассчитать зависимость Те от Е при любой температуре.
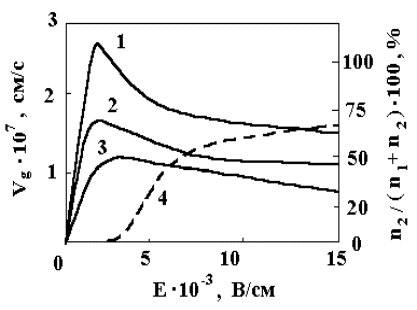
Зависимости
Здесь же штриховой линией показана зависимость заселённости верхней долины от Е. Из результатов расчёта следует, что пороговое значение напряжённости поля увеличивается с ростом температуры (см рис [2] ). Кроме того, при достаточно высокой температуре должен исчезать участок ВАХ с ОДС, так как в этом случае показатель экспоненты в (4) мал даже в области слабых полей, когда Те ~Т , и поэтому экспонента меняется незначительно при увеличении Е и Те . Но тогда как следует из (4) ,
Из (4) также следует, что плотность состояний в основном минимуме зоны проводимости должна быть мала, а в побочном - велика. В противном случае член с экспонентой в (4) будет значительно меньше единицы и не сможет эффективно влиять на величину Значения параметров, характеризующих ВАХ образцов из арсенида галлия и фосфида индия соответственно равны: напряжённость порогового поля - 3,2 * 103 и 10,5* 103 В/см максимальная величина дрейфовой скорости - 2,2* 107 и 2,5* 107 см/с максимальная величина отрицательной дифференциальной подвижности - 2400 и 2000 см2 .(В* с). | ||||||
| Лист | ||||||
| 6 | ||||||
|
Изм | Лист | № докум | Подпись | Дата | ||
| Дипольные домены и возможные режимы работы диодов Ганна . Анализ механизма возникновения периодических изменений сопротивления образца с ОДС проведём на примере однородно легированного полупроводника с омическими контактами, в котором приложенная разность потенциалов создаёт электрическое поле Е=Еп Предположим, что в некоторый момент времени вследствие тепловой флуктуации группа электронов сместилась в сторону катода относительно неподвижно ионизованных доноров (рис [3], а ). Тогда возникшая таким образом избыточная концентрация электронов (рис [3], б ) должна изменятся во времени с известным соотношением
К-во Просмотров: 397
Бесплатно скачать Реферат: АЦЭ - Разработка и расчёт автогенератора на диоде ганна с перестройкой частоты
|
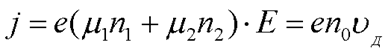 (1)
(1) 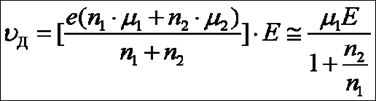 (2)
(2) 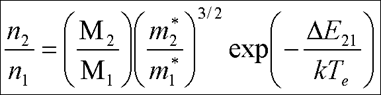 (3)
(3) 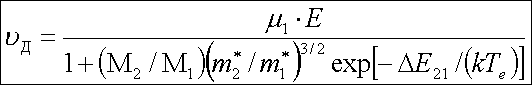 (4)
(4) 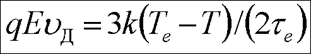 (5)
(5) 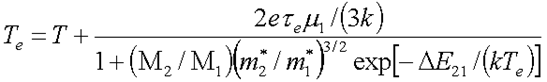 (6)
(6)