Реферат: Автоматизированное управление в технических системах

2) затраты на закупку партии;

2) затраты на хранение запасов.

Затраты на создание запаса включают расходы на оформление заказа, размещение и заключение договоров, почтовые и телеграф­ные расходы, расходы по разъездам агентов снабжения, оплату учет­ных оверашй и т.д. В первом приближении можно считать, что зат­раты на создание запаса не зависят от объема заказа Q. Обозна­чим затраты на создание запаса a , руб.

Затраты на закупку партии определяются закупочными ценами единицы запасаемого продукта и объемом партии Q . Затраты этого вида неизбежны в том случае, если необходимый продукт неп­рерывно поставляется и тут же потребляется без образования запа­са. Поэтому эти затраты не участвуют собственно в модели созда­ния и содержания запасов.

3 затраты на хранение запасов входят расходы на складские операции; амортизационные расходы использования складского помещения; потери за счет омертвления средств при хранении запаса; потери за счет порчи и морального старения хранящегося продукта; загрузочно-разгурочные, транспортные расходы и т.д. Пусть рас­ходы на хранение единицы продукта в единицу времени составляют b руб./ед.вр. Обозначим расходы в течение цикла t^Q на создание и хранение единицы продукта С. ,руб./шт. Эта величина складывается из затрат на создание в запас единицы продукта (1-я группа) и затрат на хранение единицы продукта (3-я группа).

Пусть за период Т можно произвести несколько заказов на однородный продукт с объемом каждого заказа Q. Если размер разового заказа велик, то число поставок за период Т неболь­шое, и издержки 1-й группы невелики, но при этом возрастает среднее количество хранимого запаса и возрастают затраты 3-й группы.

Если же делать заказы малыми партиями, то затраты на хране­ние небольшого запаса будут велики, но зато из-за большого коли­чества поставок в течение периода Т возрастут затраты на оформление большого числа заказов (издержки 1-й группы). Таким образом, задача определения наилучших значений Q и t^Q яв­ляются оптимизационной и суть ее сводится к отысканию оптимальных значений Q и t^Q , минимизирующих суммарные расходы на соз­дание и хранение запасов за весь плановый период Т

Рассмотрим задачу определения значений Qo и t^Q - для двух моделей: для модели без страховых запасов и для модели со страховыми запасами.

Модель без страховых запасов

Предполагается, что U и V ( u>V) - постоянные вели­чины, и в момент полного исчерпания запасов начинается новая поставка, т.е. дефицит продукта не допускается. Графически дейст­вие такой модели изображено на рис.3.1.

Уровень запасов в течение полного цикла t^Q движения запа­сов, начинающийся в момент времениt = 0 можно описать следующим образом:

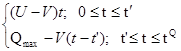(3.1.)

Примем во внимание следующие очевидные соотношения:

(3.2.)

где Q - объем заказа.

С учетом (3.2) выражение (3.1) можно переписать в виде

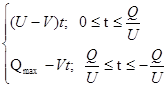(3.3.)

Определим средний объем запаса Q за цикл - t^Q :

(3.4.)

Тогда среднее время хранения единицы запасенного продукта равно

Пусть b , руб./(шт.ед.вр.), есть затраты на хранение единицы продукта в единицу времени. Тогда за цикл tQ удельные затра­ты на хранение единицы запасенного продукта, руб./шт., составят

(3.5.)

Удельныезатраты на создание в запас единицы продукта,руб./шт., равны

(3.6.)

Тогда суммарные расходы на создание и хранение единицы запаса, руб./шт., в течение цикла t^Q составят

(3.7.)

Если изобразить графически зависимость затрат на создание и содержание запасов от объема заказа Q (рис.3.2), то нетрудно убедиться, что суммарная кривая C(Q) имеет экстремум, поло­жение которого определяется соответствующими значениями величин правой части соотношения (3.7). Определим оптимальный объем заказываемой партии Q₀ . из условия

(3.8.)

Решая (3.8), получим

(3.9.)

Если постановка осуществляется мгновенно, т.е.l= 0 и U = ¥, оптимальный объем пратии равен

(3.10.)

Из сопоставления (3.10) и (3.9) следует, что при постепенной поставке заказа объем заказываемой партии должен быть больше.

Величина удельных дополнительных расходов при оптимальном объеме заказа q₀ равна

(3.11.)

Наконец, оптимальная величина интервала между соседними зака­зами составляет

(3.12.)

Модель со страховым запасом

Графически действие этой модели изображено на рис.3.3., Прив­лекая рассуждения, которые использовались при рассмотрении пре­дыдущей модели, нетрудно получить следующие результаты. Средее количество запаса Q_ср за цикл t^Q составит

(3.13)

При постоянной скорости расходования запасов V среднее время хранения единицы запасенного продукта равно

(3.14.)

Это выражение отличается от значенияtсp для предыдущей модели наличием постоянного слагаемого Q_cp /V . За цикл t^Q удельные затраты на хранение единицы запасенного продук­та, руб./шт., определяются по формуле

(3.15.)