Реферат: Бернулли

Николай(1662-1716) Иоганн I (1667-1748)

Николай

Николай I (1687-1759)

Николай II (1695-1726) Даниил I (1700-1782)

Иоганн II (1710-1790)

Якоб II (1759-1789) Иоганн III (1744-1807) Даниил II(1751-1834)

Кристоф(1782-1863)

Иоганн-Густав(1811-1863)

Якоб I. Родился 27 декабря 1654 г. По желанию отца готовился к званию протестантского священника. Окончил Базельский университет, где изучал философию, богословие и языки. Владел немецким, французским, английским, итальянским, латинским и греческим языками. Испытывая непреодолимое влечение к математике, изучал ее тайком от отца. В 1671 г. получил степень магистра философии. С большим успехом читал проповеди на немецком и французском языках. В то же время продолжал пополнять свои знания по математике без учителя, почти без учебников.

В октябре 1686 г. оказывается вакантной должность профессора математики в Базельском университете. Успехи Якоба в математике хорошо известны, и Сенат университета единодушно выдвинул на вакантную должность Якоба Бернулли. Вступление в должность состоялось 15 февраля 1687 г. Вряд ли присутствовавшие при этом скромном акте представляли, что они являются свидетелями начала беспримерного в истории математики события: отныне кафедру будут занимать Бернулли на протяжении ста лет. Члены же этой семьи будут профессорами родного университета в течение четверти тысячелетия, вплоть до второй половины XX в.

В том же году Якоб Бернулли прочитал в «Асtа Eruditirum» за 1684 г. «Новый метод» Лейбница и, обнаружив трудные места, письменно обратился к Лейбницу за разъяснением. Лейбниц, находившийся в длительной служебной поездке, получил письмо только через три года, когда надобность в консультации отпала: Якоб совместно Иоганном овладели дифференциальным и интегральным исчислениями настолько, что вскоре смогли приступить систематическому развитию метода. Образовавшийся триумвират — Лейбниц, Якоб и Иоганн Бернулли — менее чем за двадцать лет чрезвычайно обогатил анализ бесконечно малых.

С 1677 г. Я. Бернулли стал вести записные книжки, куда вносил различного рода заметки научного содержания. Первые записи посвящены теологии, сделаны под влиянием распространенного в то время в Базеле сборника спорных теологических вопросов.

Основное место в записных книжках занимает решение задач. Уже по ранним записям можно судить о проявленном Я. Бернулли интересе к прикладной математике. Математические заметки показывают, как постепенно Я. Бернулли овладевал методами Валлиса, Декарта, инфинитезимальными методами, как развивал и совершенствовал их. Решенные им задачи служили отправными пунктами для дальнейших более глубоких исследований.

В январе 1684 г. Я. Бернулли провел в Базельском университете открытый диспут, на котором защищал 100 тезисов, из них 34 логических, 18 диалектических и 48 смешанных. Некоторые тезисы крайне любопытны. Вот примеры:

«78. Иногда существует несколько кратчайших путей из точки в точку.

83. .Среди изопериметрических фигур одна может быть в бесконечное число раз больше другой.

85. Не в каждом треугольнике сумма внутренних углов равна двум прямым.

89. Квадратура круга еще не найдена, но не потому, что между искривленным и прямолинейным нет никакой связи; в действительности кривую можно спрямить, а криволинейную фигуру квадрировать»

В мае 1690 г. Я. Бернулли опубликовал в «Асtа Eruditirum» первую работу, связанную с исчислением бесконечно малых. В ней он дал решение поставленной Лейбницем в 1687 г. задачи о парацентрической изохроне. Необходимо было найти кривую, по которой материальная точка опускалась бы в равные промежутки времени на равные высоты. Я. Бернулли вывел дифференциальное уравнение кривой и проинтегрировал его. При этом он впервые употребил в печати термин «интеграл», указав, что из равенства двух выражений, связывающих дифференциалы, следует равенство интегралов.

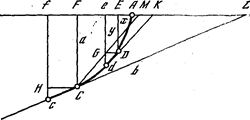В лекциях, читанных Лопиталю, И. Бернулли ход решения излагает так. Пусть искомой кривой будет АDС. Материальная точка за время ∆t перемещается из точки D в точку d и из точки С в точку с. По условию задачи проекции дуг Dd Сс на вертикаль одинаковы. Проведем через D и С касательные к кривой до пересечения с продолжением АF. Отрезки касательных будут DK и CL. Напишем тождество

Dd/Сс=Dd/Hc • Hc/Cc.

Дуги Dd и Сс малы, поэтому фигуры GDd и НСс можно считать треугольниками.

Из подобия треугольников GDd и DEK, НСс и СFL получим

Dd/DG=DK/DE,Сс/Нс=CL/СF.

С помощью этих пропорций найдем

Dd/Сс=DG1Нс • DК/DЕ • СF/СL.

По условиям задачи dG/Нс=1, поэтому

Dd1Сс=DК/DЕ • СF/СL.

Проведем через точку С прямую СМ, параллельную DК. Тогда