Реферат: Биомолекулярные вычисления
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Реферат на тему:
"Биомолекулярные вычисления"
Введение
Биомолекулярные вычисления или молекулярные компьютеры, или даже ДНК- или РНК-вычисления, – все эти термины появились на стыке таких различных наук, как молекулярная генетика и вычислительная техника.
Биомолекулярные вычисления – это собирательное название для различных техник, так или иначе связанных с ДНК или РНК. При ДНК-вычислениях данные представляются не в форме нулей и единиц, а в виде молекулярной структуры, построенной на основе спирали ДНК. Роль программного обеспечения для чтения, копирования и управления данными выполняют особые ферменты.
Основой всей системы хранения биологической информации, а стало быть, и ДНК-компьютеров, является способность атомов водорода, входящих в азотистые соединения (аденин, тимин, цитозин и гуанин), при определенных условиях притягиваться друг к другу, образуя невалентно связанные пары. С другой стороны, эти вещества могут валентно связываться с сочетаниями молекулы сахара (дезоксирибозы) и фосфата, образуя так называемые нуклеотиды. Нуклеотиды, в свою очередь, легко образуют полимеры длиной в десятки миллионов оснований. В этих супермолекулах фосфат и дезоксирибоза играют роль поддерживающей структуры (они чередуются в цепочке), а азотистые соединения кодируют информацию.
Молекула получается направленной: начинается с фосфатной группы и заканчивается дезоксирибозой. Длинные цепочки ДНК называют нитями, короткие – олигонуклеотидами.
Каждой молекуле ДНК соответствует еще одна ДНК – так называемое дополнение Ватсона – Крика. Она имеет противоположную направленность, нежели оригинальная молекула. В результате притяжения аденина к тимину и цитозина к гуанину получается знаменитая двойная спираль, обеспечивающая возможность удвоения ДНК при размножении клетки. Задача удвоения решается с помощью специального белка-энзимы – полимеразы. Синтез начинается только если с ДНК прикреплен кусочек ее дополнения, Данное свойство активно используется в молекулярной биологии и молекулярных вычислениях. По сути своей полимераза – это реализация машины Тьюринга, состоящая из двух лент и программируемого пульта управления. Пульт считывает данные с одной ленты, обрабатывает их по некоторому алгоритму и записывает на другую ленту. Полимераза также последовательно считывает исходные данные с одной ленты (ДНК) и на их основе формирует ленту с результатам вычислений (дополнение Ватсона – Крика).
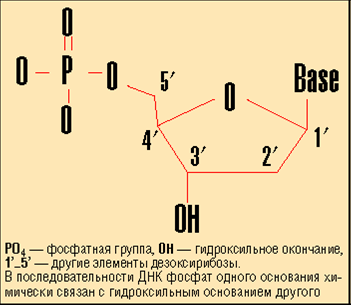
Рис. 1. Структура нуклеотида
Молекулярный компьютер – это устройство, в котором вместо кремниевых чипов, применяемых в современных компьютерах, работают молекулы и молекулярные ансамбли. Переводить молекулу из одного состояния в другое (переключать) можно с помощью света, тепла, химических агентов, электрического и магнитного поля и т.д. Фактически такие переключаемые бистабильные молекулы – это наноразмерная двухбитовая система, воспроизводящая на молекулярном уровне функцию классического транзистора.
В одном кубическом сантиметре ДНК может находиться больше информации, чем на триллионе СD. Поэтому ученые решили использовать изобретение природы и применить молекулы ДНК для хранения и обработки данных в биокомпьютерах.
Кроме того, биомолекулярный компьютер может параллельно выполнять тысячи и миллионы операций, т.е. будут работать в 1.000.000.000 быстрее. Еще одно важнейшее свойство – экономный расход энергии: ДНК-компьютер сможет совершать 10 в 19-й степени операций на джоуль израсходованной энергии – это в миллиард раз экономнее, чем в кремниевых системах.
Развитие
ДНК-вычисления впервые были с успехом применены в 1994 году Леонардом Эдлеманом, профессором Университета Южной Калифорнии, для решения задачи коммивояжера. Суть ее в том, чтобы найти маршрут движения с заданными точками старта и финиша между несколькими городами (в данном случае семь), в каждом из которых можно побывать только один раз. Эта задача решается прямым перебором, однако при увеличении числа городов сложность ее возрастает.
В пробирку помещают около 100 триллионов молекул ДНК, содержащих все возможные 20-нуклеотидные последовательности, кодирующие города и пути между ними. Затем за счет взаимного притяжения нуклеотидов отдельные цепочки ДНК сцепляются друг с другом случайным образом, а специальный фермент лигаза сшивает образующиеся короткие молекулы в более крупные образования. При этом синтезируются молекулы ДНК, воспроизводящие все возможные маршруты между городами. Остается лишь выделить среди них те, что отвечают искомому решению.
При масштабировании задачи коммивояжера возникают трудности. ДНК-компьютер Эдлемана искал оптимальный маршрут для 7 узлов. Но чем больше городов надо объехать коммивояжеру, тем больше ДНК-материала требуется биологическому компьютеру. Было подсчитано, что если увеличить количество узлов до 200, то потребуется ДНК-цепочка, вес которой превышает вес Земли.
Как он искал решение: сначала он последовательно удалил сначала цепочки, которые не начинались с первого города – точки старта – и не заканчивались местом финиша, затем те, что содержали более семи городов или не содержали хотя бы один. Легко понять, что любая из оставшихся после такого отбора молекула ДНК представляет собой решение задачи.
Вслед за работой Эдлемана последовали другие. Интересную разработку предложили израильские ученые из Вейцманновского института. Команда во главе с профессором Эхудом Шапиро решила создавать не специализированную методику для решения строго конкретной задачи, а технологию многоцелевого нанокомпьютера на базе уже известных свойств биомолекул, таких как ДНК и энзимы.
Поле деятельности не ограничено решением таких комбинаторных задач. Вскоре после опубликования работы Эдлемана разные группы начали исследования в области решения логических задач.
В 1995 г. Ричард Липтон из Принстонского университета показал, как, используя ДНК, кодировать двоичные числа и решать проблему удовлетворения логического выражения. Суть этой проблемы состоит в следующем. Пусть имеется некоторое логическое выражение F (X1, X2,…., Xn). Какие значения нужно присвоить входящим в него логическим переменным Xi, чтобы F давало истину?
Вообще говоря, задачу можно решить только перебором 2n комбинаций. И с помощью ДНК легко закодировать их все. Для этого нужно построить граф, описывающий операцию присваивания значений переменным. В нем вершины отображают единичные и нулевые значения Xi, некоторые промежуточные переменные, а пути описывают присваивание. Например, на графе для двух переменных X и Y, показанном на рисунке, путь a не-X b Y c представляет собой присваивание X = 0, Y = 1.
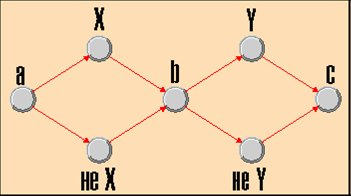
Рис. 4. Граф инициализации для задачи удовлетворения логического выражения для двух переменных
Вершины и ребра этого графа можно представить отрезками ДНК так же, как это делалось в методе Эдлемана. Перемешивание всех этих олигонуклеотидов даст раствор, содержащий ДНК, кодирующие все возможные комбинации входных параметров. Логические операции сводятся к извлечению ДНК, содержащих нужные биты в нужном месте, т.е. к нахождению пути, проходящего через конкретную вершину графа.
Рассмотрим, например, случай ![]() , и пусть E (t, i, d) – операция извлечения из трубки t всех молекул, где бит i равен d; плюсом обозначим слияние трубок, а присваиванием – переливание их содержимого. Тогда следующая последовательность операций решает поставленную задачу:
, и пусть E (t, i, d) – операция извлечения из трубки t всех молекул, где бит i равен d; плюсом обозначим слияние трубок, а присваиванием – переливание их содержимого. Тогда следующая последовательность операций решает поставленную задачу:

--> ЧИТАТЬ ПОЛНОСТЬЮ <--