Реферат: Быстрые алгоритмы сортировки
a3 = min(a3, a6)
b2 := a3
Просівання елементів відбувається доти, поки весь вихідний масив не буде заповнений символами M, тобто n раз:
For I := 1 to n do begin
Відзначити шлях від кореня до листка символом M;
Просіяти елемент уздовж відзначеного шляху;
B[I] := корінь дерева
end;
Обґрунтування правильності алгоритму очевидно, оскільки кожне чергове просівання викидає в масив У найменший з елементів масиву А, що залишилися.
Сортуюче дерево можна реалізувати, використовуючи або двовимірний масив, або одномірний масиві ST[1..N], де N = 2n-1 (див. наступний розділ). Оцінимо складність алгоритму в термінах M(n), C(n). Насамперед відзначимо, що алгоритм TreeSort працює однаково на усіх входах, так що його складність у гіршому випадку збігається зі складністю в середньому.
Припустимо, що n - ступінь 2 (n = 2l ). Тоді сортуюче дерево має l + 1 рівень (глибину l). Побудова рівня I вимагає n / 2I порівнянь і пересилань. Таким чином, I-ий етап має складність:
C1 (n) = n/2+n/4+ ... + 2+1 = n-1, M1 (n) = C1 (n) = n - 1
Для того, щоб оцінити складність II-го етапу З2 (n) і M2 (n) помітимо, що кожен шлях просівання має довжину l, тому кількість порівнянь і пересилань при просіванні одного елемента пропорційно l. Таким чином, M2 (n) = O(l n), C2 (n) = O(l n).
Оскільки l = log2 n, M2 (n)=O(n log2 n)), C2 (n)=O(n log2 n), Але З(n) = C1 (n) + C2 (n), M(n) = M1 (n) + M2 (n). Тому що C1 (n) < C2 (n), M1 (n) < M2 (n), остаточно одержуємо оцінки складності алгоритму TreeSort за часом:
M(n) = O(n log2 n), C(n) = O(n log2 n),
У загальному випадку, коли n не є ступенем 2, сортуюче дерево будується трохи інакше. “Зайвий” елемент (елемент, для якого немає пари) переноситься на наступний рівень. Легко бачити, що при цьому глибина сортуючого дерева дорівнює [log 2 n] + 1. Удосконалення алгоритму II етапу очевидно. Оцінки при цьому змінюють лише мультиплікативні множники. Алгоритм TreeSort має істотний недолік: для нього потрібно додаткова пам'ять розміру 2n - 1.
1.2. Пірамідальне сортування
Алгоритм пірамідального сортування HeapSort також використовує представлення масиву у виді дерева. Цей алгоритм не вимагає допоміжних масивів, сортуючи “на місці”. Розглянемо спочатку метод представлення масиву у виді дерева:
Нехай A[1 .. n] - деякий масив. Зіставимо йому дерево, використовуючи наступні правила:
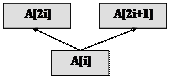 1.A[1] - корінь дерева ;
1.A[1] - корінь дерева ;
2.Якщо A[i] - вузол дерева і 2i £n,
то A[2*i] - вузол - “лівий син” вузла A[i]
3.Якщо A[i] - вузол дерева і 2i + 1 £ n,
то A[2*i+1] - вузол - “правий син” вузла A[i]
Правила 1-3 визначають у масиві структуру дерева, причому глибина дерева не перевершує [log2 n] + 1. Вони ж задають спосіб руху по дереву від кореня до листків. Рух вгору задається правилом 4:
4.Якщо A[i] - вузол дерева і i > 1,
то A[i mod 2] - вузол - “батько” вузла A[i];
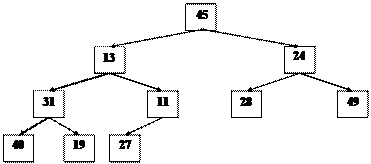 |
???????: ????? A = [45 13 24 31 11 28 49 40 19 27] - ?????. ³???????? ???? ?????? ??? ???:
Зверніть увагу на те, що всі рівні дерева, за винятком останнього, цілком заповнені, останній рівень заповнений ліворуч і індексація елементів масиву здійснюється вниз і праворуч. Тому дерево упорядкованого масиву відповідає наступним властивостям:
A[i] ( A[2*i], A[i] ( A[2*i+1], A[2*i] ( A[2*i+1].