Реферат: Частотные характеристики линейных систем управления
![]() - действительная частотная характеристика;
- действительная частотная характеристика;
![]() - мнимая частотная характеристика;
- мнимая частотная характеристика;
![]() - амплитудная частотная характеристика;
- амплитудная частотная характеристика;
![]() - фазовая частотная характеристика.
- фазовая частотная характеристика.
Пусть теперь ![]() . Эта функция отличается от ранее рассмотренной функции
. Эта функция отличается от ранее рассмотренной функции ![]() только знаком частоты. Частотная характеристика является комплексным коэффициентом усиления для любой частоты, в том числе и отрицательной. Поэтому для определения соответствующего выходного воздействия
только знаком частоты. Частотная характеристика является комплексным коэффициентом усиления для любой частоты, в том числе и отрицательной. Поэтому для определения соответствующего выходного воздействия ![]() достаточно сменить знак частоты в выражении (13)
достаточно сменить знак частоты в выражении (13)
![]() . (15)
. (15)
Если входной процесс равен сумме этих воздействий (11), то выходной процесс равен сумме соответствующих выходных процессов (13) и (15).
Проделав ряд элементарных преобразований
![]()
![]() (16)
(16)
получим, что при гармоническом входном воздействии выходной процесс также гармонический, амплитуда которого в ![]() раз больше амплитуды входного воздействия, а фаза больше фазы входного воздействия на
раз больше амплитуды входного воздействия, а фаза больше фазы входного воздействия на ![]() .
.
Здесь использовано свойство четности амплитудной частотной характеристики, которое легко следует из выражений связи между различными ее составляющими
![]() ,
, 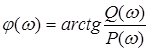 ,
,
![]() ,
, ![]() (17)
(17)
Не трудно убедиться, что соотношения между различными частотными характеристиками системы такие же, как и между различными составляющими комплексного числа.
Из всего сказанного следует, что если входной процесс представлен рядом Фурье, то для определения ряда Фурье выходного процесса достаточно изменить описанным выше образом амплитуды и фазы входного процесса.
Еще проще определяется преобразование Фурье ![]() выходного процесса
выходного процесса ![]() по преобразованию Фурье
по преобразованию Фурье ![]() входного процесса
входного процесса ![]() . Как не трудно показать,
. Как не трудно показать,
![]() . (17)
. (17)
Для этого только достаточно вспомнить формальное определение и содержательный смысл преобразования Фурье. С формальной точки зрения для любой абсолютно интегрируемой функции ![]() , т.е. функции для которой
, т.е. функции для которой
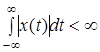 ,
,
существует прямое и обратное преобразования Фурье
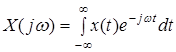 ,
, 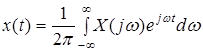 .
.
Последнее выражение и позволяет трактовать преобразование Фурье некоторой функции времени в виде суммы гармоник ![]() с комплексными «амплитудами»
с комплексными «амплитудами» ![]() . Преобразование каждой такой гармоники сводится к умножению ее «амплитуды» на комплексный коэффициент усиления
. Преобразование каждой такой гармоники сводится к умножению ее «амплитуды» на комплексный коэффициент усиления ![]() , как показывает выражение (17).
, как показывает выражение (17).
Преобразование Фурье обладает одним существенным с теоретической точки зрения недостатком – его нельзя применить к функциям, которые не являются абсолютно интегрируемыми. Таких функций достаточно много, чтобы в полной мере ощутить неудобство данного ограничения. Например, функция – константа, сохраняющая постоянное ненулевое значение сколь угодно долго, не является абсолютно интегрируемой. Вместе с тем, такая функция простейшим образом описывает постоянное воздействие.
Этого недостатка лишено преобразование Лапласа, которое широко используется в классической теории управления. Оно является обобщением преобразования Фурье, на его основе дается определение центрального понятия классической теории управления, понятия передаточной функции. Последняя является обобщением только что введенного понятия частотной характеристики в той же мере, в какой преобразование Лапласа является обобщением преобразования Фурье.
Эти понятия настолько тесно связаны между собой, что иногда их не различают. Например, не смотря на то, что центральным понятием классической теории автоматического управления является, как у же отмечалось, понятие передаточной функции, методы этой теории называются частотными. На наш взгляд, это происходит потому, что использование именно преобразования Лапласа связано с вычислительной стороной дела, но как только дело доходит до физической интерпретации результатов, полученных с помощью передаточных функций, переходят к частотным характеристикам.
ЛИТЕРАТУРА
1. Мирошник И.В. Теория автоматического управления. Линейные системы. - СПб.: Питер, 2005.
2. Филлипс Ч., Харбор Р. Системы управления с обратной связью. М.: Лаборатория Базовых Знаний, 2001.