Реферат: Численное интегрирование определённых интегралов

Раскроем скобки:

Это и есть «большая формула Симпсона». Её точность, также как и у всех формул рассмотренных выше, тем выше, чем больше n. Эта формула совпадает с формулой (7), выведенной с помощью парабол. Для оценки погрешности формулы Симпсона используется формула: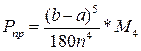

Качество этой формулы лучше, чем формулы трапеции и прямоугольников, так как при одном и том же n она даёт большую точность.

ПРАКТИКА

Общий вид интеграла, решение которого, будет рассмотрено в этом разделе: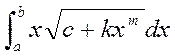

Заданные значения:

a=0; c=0,3; m=2; b=3; k=7.

Подставим заданные значения:

.
Сначала, решим искомый интеграл напрямую, основываясь на полученные ранее знания.

Применим метод замены:

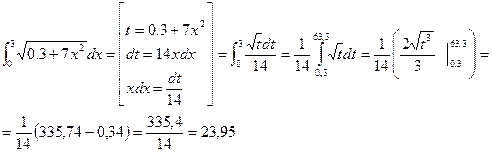
Разделим отрезок [0;3] на n=10 равных частей и найдём шаг деления: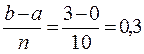

Найдём значение подынтегральной функции:

X	Y
0	0
0,3	0,289
0,6	1,007
0,9	2,199
1,2	3,866
1,5	6,009
1,8	8,628
2,1	11,724
2,4	15,296
2,7	19,344
3	23,868

ФОРМУЛА ПРЯМОУГОЛЬНИКОВ :

1.Входящих

2.Выходящих

3.Средних

X	Y
0,15	0,101458
0,45	0,58974
0,75	1,543889
1,05	2,973095
1,35	4,878247
1,65	7,259531
1,95	10,11701
2,25	13,45069
2,55	17,2606
2,85	21,54674

Определим погрешность метода прямоугольников:

P_np =

М₂ – максимальное значение второй производной на данном промежутке.

ФОРМУЛА ТРАПЕЦИЙ

Определим погрешность метода трапеции:

М₂ – максимальное значение второй производной на данном промежутке.

ФОРМУЛА СИМПСОНА