Реферат: Численное решение модельного уравнения

Для функции (13):

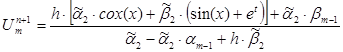
Данные функции тестировались на отрезке по X: [0, 1] , по времени: [0, 1], с количеством разбиений по этим отрезкам - 30 .

3. МЕТОДИКА РЕШЕНИЯ ТЕСТОВЫХ ЗАДАЧ

Данная задача решается с помощью двухслойной неявно конечно-разностной схемы.

Схема реализуется в три этапа.

1 этап: находятся предварительные значения с помощью 4-х точечной неявной схемы:

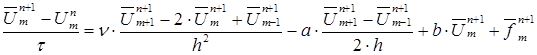( 5 )

2 этап: используется за два шага. Сначала находятся на полученном слое () с шагом , а затем через . В этом случае используется 4-х точечная неявная разностная схема:

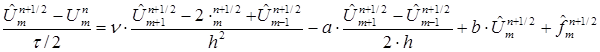( 6 )

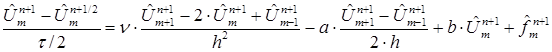( 7 )

3 этап: окончательные значения находятся в виде линейной комбинации двух предварительных значений:

( 8 )

Для решения (1) воспользуемся формулами (5) - (8). Данные уравнения представляют трех диагональные матрицы, решаемые методом скалярной прогонки.

В начале нужно преобразовать (5) – (7) к виду:

( 14 )

Тогда (5) примет вид:

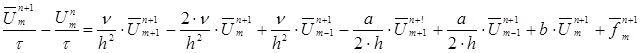
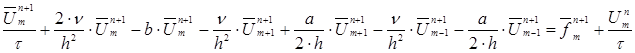
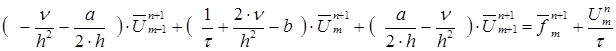
Т.е. ;

;

;

.

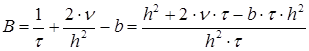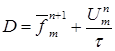Формула (6) преобразуется в:

Т.е. ;

;

;

.

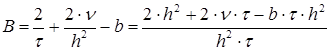Формула (7) преобразуется в:

Т.е. ;

;

;

.

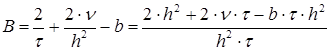Далее решаем по формулам скалярной прогонки:

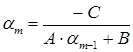
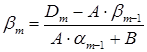( 15 )

( 16 )

Для определения , и воспользуемся данными граничными условиями, т.е. формулой (4) и функцией . Так если мы берём из формулы (9), то имеем:

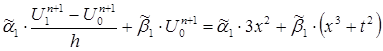
Приведём это выражение к виду: .

?.?. ?????? ?? ????? ? :