Реферат: Диалектика развития понятия функции. Различные подходы к изучению функций в школе и исследования

Затем дается первое определение зависимой и независимой переменных:

“Переменную a , значения которой выбираются произвольно, называют независимой переменной , а переменную S , значения которой определяются выбранными значениями a , -зависимой переменной ”.

“ П р и м е р 2. На рисунке 2 изображен график температуры воздуха в течении суток.

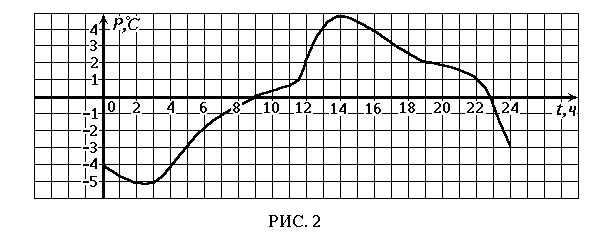
С помощью этого графика для каждого момента времени t (в часах), где 0 £t £ 24, можно найти соответствующую температуру p (в градусах Цельсия). Например,

если t = 6, то p = -2;

если t = 12, то p = 2;

если t = 17, то p = 3;

Здесь t является независимой переменной, а p - зависимой переменной.

П р и м е р 3. Стоимость проезда в пригородном поезде зависит от номера зоны, к которой относится станция. Эта зависимость показана в таблице (буквой n обозначен номер зоны, а буквой m - соответствующая стоимость проезда в тысячах рублей):

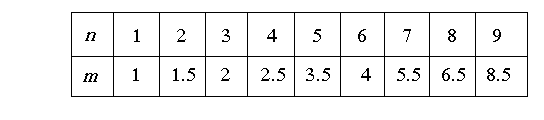
По этой таблице для каждого значения n , где n = 1, 2, ..., 9, можно найти соответствующее значение m . Так,

если n = 2, то m = 1.5;

если n = 6, то m = 4 ;

если n = 9, то m = 8.5;

В этом случае n является независимой переменной, а m - зависимой переменной.”

Обилие примеров, призванных проиллюстрировать понятие функции, объясняется тем фактом, что проводя аналогии между различными примерами, учащиеся интуитивно нащупывают суть этого понятия, строят догадку относительно функциональных зависимостей в быту и в природе, и получают ее подтверждение в последующих примерах. Второй не менее важной причиной является то, что каждый из этих примеров содержит функцию заданную одним из возможных способов. В первом примере она задана аналитически, во втором - графически, в третьем это таблица. Это не случайность, разбирая примеры вместе с учителем, дети сразу привыкают к различным способам задания функций. И когда преподаватель начнет рассказывать параграф о способах задания функций, ученикам будет гораздо легче осознать новый материал, потому что для них он не будет абсолютно новым - они уже сталкивались с этим ранее.

Далее дается само определение функции, вводятся термины аргумент и значение функции .

“В рассмотренных примерах каждому значению независимой переменной соответствует единственное значение зависимой переменной. Такую зависимость одной переменной от другой называют функциональной зависимостью или функцией .

Независимую переменную иначе называют аргументом , а о зависимой переменной говорят, что она является функцией от этого аргумента. Так, площадь квадрата является функцией от длины его стороны; путь, пройденный автомобилем с постоянной скоростью, является функцией от времени движения. Значения зависимой переменной называют значениями функции .

Все значения которые принимает независимая переменная, образуют область определения функции .”

Так на практике реализуется индуктивный подход к изучению функций в школе. Альтернативой ему служит дедуктивный подход, который, хотя и применяется реже, имеет целый ряд положительных аспектов, которые и стали причиной его применения в школе. Для этого подхода характерно первоначальное полное и сжатое изложение учебного материала, пускай даже малопонятного при первом прочтении, и дальнейшая углубленная проработка всех примеров, терминов и определений. Такой подход к изучению функций и не только их позволяет учащимся самостоятельно попытаться проследить логические связи в излагаемом материале, резко увеличивает интенсивность мыслительной деятельности, способствует более активному и глубокому запоминанию. Вот как выглядит изложение той же темы “Понятие функции” в соответствии с дедуктивным подходом:

1. Зависимости одной переменной от другой называют функциональными зависимостями.

2. Зависимость переменной у от переменной х называют функцией, если каждому значению х соответствует единственное значение у . При этом используют запись у = f (х ).

3. Переменную х называют независимой переменной или аргументом, а переменную у - зависимой переменной. Говорят, что у является функцией от х .

4. Значение у , соответствующее заданному значению х , называют значением функции.

5. Все значения, которые принимает независимая переменная, образуют область определения функции; все значения, которые принимает зависимая переменная, образуют множество значений функции.

6. Для функции f приняты обозначения: D ( f ) -область определения функции, E ( f ) - множество значений функции, f (х 0) - значение функции в точке х 0.

7. Если D ( f ) ÌR и E ( f ) ÌR , то функцию называют числовой.

8. Элементы множества D ( f ) также называют значениями аргумента, а соответствующие им элементы E ( f ) - значениями функции.

9. Если функция задана формулой и область определения функции не указана, то считают, что область определения состоит из всех значений независимой переменной, при которых эта формула имеет смысл.

10. Графиком функции называют множество всех точек, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции.

Затем, на следующих уроках, происходит детальный разбор этого материала при активной работе учащихся. Тщательно рассматриваются все определения, прорешиваются примеры - идет усвоение нового материала.

Рассмотренные выше подходы к изучению функций в школе не охватывают все многообразие способов и методов изучения этого понятия. Они лишь являются основными, наиболее разработанными подходами к вопросу об изучении функций в школе, ориентируясь на которые можно разрабатывать новые, специфические методы обучения, которые были бы лишены недостатков вышеперечисленных подходов и были бы следующим шагом в деле обучения математике в школе.

ИССЛЕДОВАНИЕ ФУНКЦИЙ С ПОМОЩЬЮ ЭВМ

История алгебры насчитывает не одну тысячу лет, и все открытия и достижения в этой области человеческого знания были получены только с помощью тяжелого умственного труда, не в последнюю очередь связанного с огромным объемом вычислений, которые приходилось производить, часто неоднократно, для получения желаемых результатов. Многим известным математикам, от древности и вплоть до нашего века, приходилось содержать целый штат вычислителей, которые выполняли огромный объем второстепенных вычислений, давая возможность ученому заниматься непосредственно развитием математической науки.