Реферат: Дифференциальные уравнения с разрывной правой частью
Рассмотрим уравнение или систему в векторной записи
![]() , (1)
, (1)
с кусочно-непрерывной функцией f в области G ;![]() ,
, ![]() , M – множество (меры нуль) точек разрыва функции f .
, M – множество (меры нуль) точек разрыва функции f .
Большинство известных определений решения уравнения (1) могут быть изложены следующим образом. Для каждой точки ![]() области G указывается множество
области G указывается множество ![]() в n -мерном пространстве. Если в точке (t,x) функция f непрерывна, то множество
в n -мерном пространстве. Если в точке (t,x) функция f непрерывна, то множество ![]() состоит из одной точки, совпадающей со значением функции f в этой точке. Если же
состоит из одной точки, совпадающей со значением функции f в этой точке. Если же ![]() -точка разрыва функции f , то множество
-точка разрыва функции f , то множество ![]() задается тем или иным способом.
задается тем или иным способом.
Определение2. Решением уравнения (1) называется решение дифференциального включения
![]() , (2)
, (2)
т.е. абсолютно непрерывная вектор-функция x(t) , определенная на интервале или отрезке I , для которого почти всюду на I
![]() .
.
Другими словами, решение дифференциального уравнения (1) определяется как функция, у которой производная ![]() может принимать любые значения из некоторого множества
может принимать любые значения из некоторого множества ![]() .
.
Иногда (2) называют диф. уравнением с многозначной правой частью. Функцию ![]() называют многозначной функцией, подчеркивая, что значение
называют многозначной функцией, подчеркивая, что значение![]() - множество. Если для всех ( t , x ) множество
- множество. Если для всех ( t , x ) множество![]() состоит из единственной точки, то (2) – обычное диф. уравнение. Функция
состоит из единственной точки, то (2) – обычное диф. уравнение. Функция ![]() называется однозначной в точке
называется однозначной в точке ![]() , если множество F
, если множество F ![]() состоит из единственной точки.
состоит из единственной точки.
Одним из наиболее популярных определений решения разрывной системы является определение А.Ф. Филиппова.
А. Выпуклое доопределение.
Применимо, в частности, к системам с малым запаздыванием того или иного рода, а также к некоторым системам с сухим трением.
Для каждой точки ![]() пусть
пусть ![]() - наименьшее выпуклое замкнутое множество, содержащее все предельные значения вектор-функции
- наименьшее выпуклое замкнутое множество, содержащее все предельные значения вектор-функции![]() , когда
, когда ![]()
![]() Решением уравнения (1) называется решение включения (2) с только что построенным
Решением уравнения (1) называется решение включения (2) с только что построенным ![]() . Т.к.
. Т.к. ![]() - множество меры нуль, то при почти всех
- множество меры нуль, то при почти всех ![]() мера сечения множества
мера сечения множества ![]() плоскостью
плоскостью ![]() равна нулю. При таких
равна нулю. При таких ![]() множество
множество ![]() определено для всех
определено для всех ![]()
![]() . В точках непрерывности функции
. В точках непрерывности функции ![]() множество
множество ![]() состоит из одной точки
состоит из одной точки ![]() и решение удовлетворяет уравнению (1) в обычном смысле. Если же точка
и решение удовлетворяет уравнению (1) в обычном смысле. Если же точка ![]()
![]() лежит на границах сечений двух или нескольких областей
лежит на границах сечений двух или нескольких областей ![]() , …,
, …, ![]() плоскостью
плоскостью ![]() , то множество
, то множество ![]() есть отрезок, выпуклый многоугольник или многогранник с вершинами
есть отрезок, выпуклый многоугольник или многогранник с вершинами ![]()
![]() ,
, ![]() , где
, где
![]()
![]() =
= ![]()
![]() .
.
Все точки ![]()
![]() (
(![]() = 1, … ,
= 1, … , ![]() содержатся в
содержатся в ![]() , но не обязательно, чтобы все они являлись вершинами.
, но не обязательно, чтобы все они являлись вершинами.
Определение 3.
Вектор-функция ![]() , определенная на интервале
, определенная на интервале ![]() называется решением уравнения (1), если она абсолютно непрерывна и если при почти всех
называется решением уравнения (1), если она абсолютно непрерывна и если при почти всех ![]() для любого
для любого ![]() вектор
вектор ![]() принадлежит наименьшему выпуклому замкнутому множеству (
принадлежит наименьшему выпуклому замкнутому множеству (![]() -мерного пространства), содержащему все значения вектор-функции
-мерного пространства), содержащему все значения вектор-функции ![]() , когда
, когда ![]() пробегает почти всю
пробегает почти всю ![]() -окрестность точки
-окрестность точки ![]() в пространстве X (при фиксированном
в пространстве X (при фиксированном ![]() ), т.е. всю окрестность, кроме множества мера нуль.
), т.е. всю окрестность, кроме множества мера нуль.
Такое определение дает однозначное продолжение решения по поверхности разрыва.
Рассмотрим случай, когда функция ![]() разрывна на гладкой поверхности
разрывна на гладкой поверхности ![]() , задаваемой уравнением
, задаваемой уравнением ![]() . Поверхность S делит свою окрестность в пространстве на области
. Поверхность S делит свою окрестность в пространстве на области ![]() и
и ![]() . Пусть при
. Пусть при ![]() и приближении
и приближении ![]() к
к ![]() из областей
из областей ![]() и
и ![]() функция имеет предельные значения
функция имеет предельные значения
![]()
![]()
Тогда множество ![]() , о котором говорится в доопределении А, есть отрезок, соединяющий концы векторов
, о котором говорится в доопределении А, есть отрезок, соединяющий концы векторов ![]() и
и ![]() , проведенных из точки
, проведенных из точки ![]() .
.
aЕсли этот отрезок при ![]() лежит по одну сторону от плоскости
лежит по одну сторону от плоскости ![]() , касательной к поверхности
, касательной к поверхности ![]() в точке, то решения при этих
в точке, то решения при этих ![]() переходят с одной стороны поверхности
переходят с одной стороны поверхности ![]() на другую:
на другую:
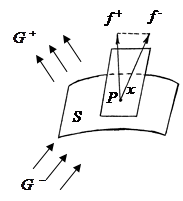
Рис. 1.
aЕсли этот отрезок пересекается с плоскостью ![]() , то точка пересечения является концом вектора
, то точка пересечения является концом вектора ![]() , определяющего скорость движения
, определяющего скорость движения
![]() (3)
(3)
по поверхности ![]() в пространстве
в пространстве ![]() :
:
|
|
|
|
|
|
|
|