Реферат: Дифракционная структура изображения. Критерии качества оптического изображения

Однако расчеты показывают, что не для всех типов аберраций это справедливо. Кроме того, для более строгого анализа нужно проверить на сколько изменится число Штреля при или . Релеевский допуск точного ответа на этот вопрос не дает.

Формула Марешаля. Допуск Марешаля для малых аберраций

Французский оптик Марешаль получил свое аналитическое выражение и свой допуск в виде среднеквадратичного по зрачку значения волновой аберрации. Критерий Марешаля более универсальный, чем допуск Релея, он подходит для любых типов аберраций.

Рассмотрим вывод формулы Марешаля. Функция рассеяния точки:

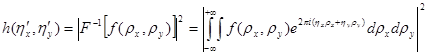. (10)

Значение ФРТ в ее центральном максимуме:

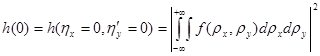. (11)

Воспользовавшись выражением для зрачковой функции, получим:

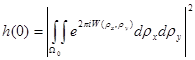. (12)

В случае малых аберраций , следовательно . Тогда при разложении функции в ряд, можно оставить только три члена, а остальные отбросить , отсюда:

. (13)

Тогда можно записать приближенное выражение для ФРТ:

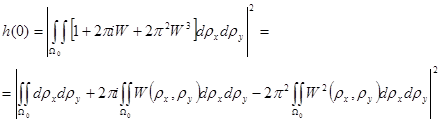. (14)

Введем обозначение для среднего значения волновой аберрации по зрачку:

(15)

и среднего квадрата волновой аберрации:

. (16)

Тогда выражение (9.48) запишется в виде:

. (17)

Модуль комплексного числа вычисляется как сумма квадратов вещественной и мнимой частей , следовательно:

. (18)

Значение ФРТ в максимуме при отсутствии аберраций определяется выражением:

. (19)

Тогда формула Марешаля:

. (20)

Величина называется дисперсией волновой аберрации по зрачку (дисперсия – это разность среднего квадрата и квадрата среднего значения):

. (21)

Формула Марешаля показывает, что важна не сама волновая аберрация, а ее изменение (деформация волнового фронта) по зрачку.

Средний квадрат деформации волнового фронта – это квадратный корень из дисперсии:

. (22)