Реферат: Дискретная математика
19.
К каким видам относятся следующие множества:
а) А - множества ИС в АЛУ; В - множества квадратньгх целых чисел. С={х: 2х-З=О}; Д={х: у - дерево, растущее на Луне}
б) А - множество МП в УУ; В - .множество простых чисел; С={у: 3у-7=0}; Д={z: z - слон без хобота}?
20.
Сколько различных семибуквенных слов можно составить из букв русского языка, не обращая внимания на их семантику?
21.
Представьте бинарное отношение, задание графом

как множество упорядоченных пар и запишите его матрицу. Какими свойствами характеризуется данное отношение?
стр. 4-1
1.
Покажите, что для любого рефлексивного отношения А отношения А È А-1 и АÇА" являются толерантностями.
2.
В общем случае объединение отношений эквивалентности А и В не является эквивалентностью. Приведите примеры, подтверждающие это положение.
3
Найти число способов распределения студенческой группы из 23 человек на бригады по 3 и 5 человек.
4.
Покажите, что композиция А*В антирефлексивных отношений А и В тогда и только тогда антирефлексивна, когда АÇВ-1 =0 .
5.
Докажите тождество: ![]()
8.
Сколько различных фигур можно изобразить с всевозможных комбинаций из элементов а, б, в,..., и почтового индекса если в каждой комбинации может присутствовать от 0 до 9 элементов
9.
Определить число всевозможных слов длины 5, если А=Х1....,Х5-алфавит.
10.
Какие из приведенных ниже выражений неверны и почему:
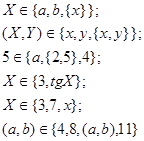
11.
Доказать, что на множестве всех групп 2-го курса факультета АВТ нужно 3 вопроса студенту, па которые он отвечает "Да" или "Нет', можно определить шифр его группы.
13.
Записать в виде теор. множественных соотношений следующие утверждения: -среди деталей первого узла имеются все пластмассовые детали -одинаковый детали, входящие в оба узла могут быть только пластмассовыми -во втором узле нет пластмассовых деталей При записи учесть, что M1 иМ2, соответственно, множества деталей 1-го и 2-го узла, А – множество пластмассовых деталей.
16.
Связаны лн множества А и В отношением включения (если ДА, то укажите какое из них является подмножеством другого):
a) A={a.b.d}, B={b,d.a,c}, А={a,c,d,e},В={а,с,е},
b) А={c,d,e},В={а,с}, A={a,(c,d),e}, B={a.e,(c, d),k}.
19.
Представьте в виде композиции функций функцию 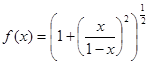
20.
Покажите, что следующая функция имеет обратные ей функции: ![]()
Найти области определения и значения обратной функции и начертить их графики.
21.
Исходя из определения дизъюнктивной суммы, покажите ее свойства (коммутативность, ассоциативность, дистрибутивность пересечения относительно симметрии разности).
22.
Доказать справедливость: ![]()
![]()
/конец стр. 4-2/
/стр. 7-1/
Вопросы по разделу " Основы теории множеств".
1.
Сколько различны х трехбуквенных слоев можно составить из букв русского алфавита, не обращая внимания на их смысл .
2.
Сколько покрывающих деревьев можно образовать, если символ каждого дерева имеет длину 15.
3.
Доказать, что для конеч ного мн-ва из n - элементов , множество всех его подмножеств содержит 2n элементов.
4. /вставить рисунок/
Сколько различных фигур можно изобразить с помощью всевозмо жны х комбинаций и з элементов " а, б,.., и почт ового индекса, если в каждой комбинации может присутствовать от 0 до 9 элементов.
5.
Покажите, что для любого множества М справедливы соотнош ения:
![]() Æ, М ÅÆ = М.
Æ, М ÅÆ = М.
6.
Покажите, что для любы х множеств А и В справедливо соотношение
![]()
7.
Покажите, что из соотношения ![]() следует СÌ A и C Ì B.
следует СÌ A и C Ì B.
8
Запишите множество упорядоченных пар ( x,y), выражающих отношение " x - делитель y " на множестве целых чисел от 2 до 10 включительно? Является ли это отношение функцией? Обладает ли оно свойством транзитивности?