Реферат: Дисперсность

Физический смысл коэффициента диффузии D: если -=1, В = 1 и t = 1, то m = D , т.е. коэффициент диффузии численно равен массе диффундирующего вещества, когда градиент концентрации, площадь сечения диффузионного потока и время равны единице. Равенство только численное, т.к. размерность коэффициента диффузии [м² /с] не соответствует размерности массы.

2) для нестационарного процесса: ¹const. Тогда интегрирование основного уравнения с учетом изменения градиента концентрации усложняется. При отсутствии в среде градиентов температуры, давления, электрического потенциала из уравнения определим массу вещества m₁ , переносимого в результате диффузии в единицу времени через единицу площади поверхности, перпендикулярной направлению переноса (В = 1 и t = 1): , с учетом которого можно определить пространственно-временное распределение концентрации:

- второй закон Фика.

На рис. представлена одномерная диффузия, определяющая движение вещества в одном направлении. Возможна также двух- и трехмерная диффузия вещества (диффузия вещества в двух и трех направлениях), описываемая уравнением: , где I – вектор плотности диффузионного потока; gradv – градиент поля концентрации.

Для трехмерной диффузии, по второму закону Фика, запишем: .

Для двумерной диффузии в правой части уравнения ограничиваемся выражениями для х и y .

Значения коэффициента диффузии для видов её распределяются так: ионная – D = 10^-8 м² /с; молекулярная - D = 10^-9 ; коллоидных частиц - D = 10^-10 . Отсюда видно, что диффузия коллоидных частиц затруднена по сравнению с двумя другими видами. Так, скорость диффузии частиц карамели (дисперсная фаза – коллоидный раствор) в 100 – 1000 раз меньше скорости диффузии молекул сахара (молекулярный раствор). Соответственно в газах D увеличивается до 10^-4 , в твердых телах снижается до 10^-12 м² /с.

Количественно диффузия определяется коэффициентом диффузии, связанным со средним сдвигом соотношением: ; - продолжительность диффузии.

Диффузия высокодисперсных частиц совершается беспорядочно с большей вероятностью в сторону меньшей концентрации. При выводе соотношения приняты следующие допущения: частицы дисперсной фазы движутся независимо друг от друга, между ними отсутствует взаимодействие; средняя энергия поступательных движений частиц равна 0,5 kT .

Используя формулу определения среднего сдвига, коэффициент диффузии можно представить в виде: (k – константа Больцмана, равная ). Если D известен, найдем размер частиц:

; Þ чем больше размер частиц, тем меньше коэффициент диффузии, менее интенсивна сама диффузия.

Диффузия в полной мере проявляется у высокодисперсных систем (10^-9 – 10^-7 м), ослаблена у среднедисперсных (10^-7 – 10^-5 м) и практически отсутствует у грубодисперсных систем (>10^-5 м). Коэффициент диффузии зависит и от формы частиц, что не учтено в уравнении . Поэтому формула определяет размер только коллоидных шарообразных частиц (или приведенный к шарообразному размер частиц неправильной формы).

Тема 1.2.3. Осмотическое давление

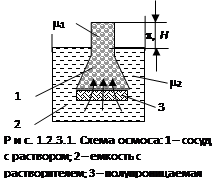При разделении двух растворов различной концентрации или раствора и чистого растворителя полупроницаемой перегородкой (мембраной) возникает поток растворителя от меньшей концентрации к большей, выравнивающей концентрацию. Этот процесс называется осмосом .

На схеме (рис. 1.2.3.1) в сосуд с полупроницаемой перегородкой 3, помещен раствор 1. Перегородка пропускает дисперсионную среду (растворитель), но является препятствием для коллоидных частиц (растворенных веществ). Снаружи перегородки – чистый растворитель 2. Концентрация раствора по обе стороны перегородки различна. Внутри сосуда 1 часть раствора занимают молекулы растворенного вещества (частицы дисперсной фазы) Þ концентрация растворителя там меньше, чем в емкости 2 с чистым растворителем.

За счет диффузии жидкость из области более высокой концентрации перемещается в область меньшей концентрации (из емкости 2 в сосуд 1). С кинетической точки зрения это обусловлено тем, что число ударов молекул о мембрану растворителя со стороны чистого или более разбавленного раствора больше, чем со стороны раствора, что и заставляет перемещаться растворитель через поры мембраны туда, где его меньше (т.е. в область раствора).

С термодинамической точки зрения , химический потенциал m₂ чистой жидкости больше m₁ растворителя в растворе, процесс самопроизвольно идет в сторону меньшего химического потенциала до их выравнивания: m₂ = m₁ .

В результате перемещения жидкости в емкости 1 создается избыточное давление p, называемое осмотическим. Растворитель, проникающий в область раствора 1, поднимает уровень жидкости на высоту Н , что компенсирует давление чистого растворителя в сторону раствора. Наступает момент, когда вес столба жидкости в области раствора уравнивается давлением растворителя.

Осмотическое давление – такое избыточное давление над раствором, которое необходимо для исключения переноса растворителя через мембрану. Осмотическое давление равно тому давлению, которое производила бы дисперсная фаза (растворенное вещество), если бы она в виде газа при той же температуре занимала тот же объем, что и коллоидная система (раствор)

Осмотическое давление p достаточно разбавленных коллоидных растворов может быть найдено по уравнению:

или - уравнение Вант-Гоффа

где m _{общ/ m} – масса растворенного вещества; m – масса одной частицы; V – объем частицы; N_A – число Авогадро; Т – абсолютная температура; n - частичная концентрация; k – постоянная Больцмана; М – масса одного моля растворенного вещества; с – массовая концентрация.