Реферат: Дисциплины обслуживания вызовов. Простейшая модель обслуживания

Дифференцируя, получаем плотность распределения вероятностей: .

Случайная величина с такой плотностью вероятностей называется экспоненциально - распределенной (с показательным распределением). Математическое ожидание экспоненциально распределенной случайной величины равно

,

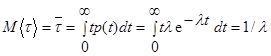а дисперсия и среднеквадратическое отклонение соответственно будут равны:

,

.

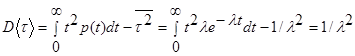Определим математическое ожидание и дисперсию числа требований за промежуток t :

,

.

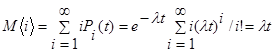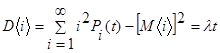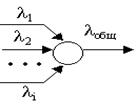
Одним из важных свойств пуассоновского потока является аддитивность.

Если образовать поток заявок как объединенный из нескольких пуассоновских потоков, то его суммарная интенсивность будет равна сумме интенсивностей каждого отдельного потока _.

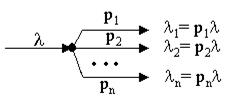
При разъединении пуассоновского потока на несколько потоков так, что каждое требование исходного потока с вероятностью p _i ( Sp _i = 1) поступает на i- тоенаправление, поток i направления будет также пуассоновским с интенсивностью lp _i .

Нестационарный пуассоновский поток

Это ординарный поток без последействия, для которого в любой момент времени существует конечный параметр потока λ(t). Пусть P_i (t₀ ,τ) – вероятность поступления i -требований за интервал [t₀ ,t₀ +τ ], которая определяется формулой:

, где .

Этот параметр имеет смысл среднего числа требований на промежутке [t₀ ,t₀ +τ]. Средняя интенсивность определяется как: .

Выбором закона изменения λ(t) можно описать реальные потоки заявок на АТС (например, отразить наличие ЧНН).

Стационарный поток без последействия.

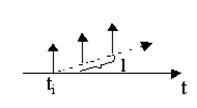Это неординарный (групповой) пуассоновский поток. События – моменты вызовов , представляют собой простейший пуассоновский поток с параметром λ . В каждый момент времени t_i с вероятностью p_l поступает группа из l ( l = 1,2 ,…r ) одинаковых заявок. Величинаl – характеристика неординарности. Обозначим параметр a_l = λp_l . Вероятность поступления k требований в промежутке времени длиной t :

.

Суммирование в этой формуле производится по всем j , удовлетворяющим соотношению: .

Это означает, что любой неординарный пуассоновский поток можно представить как k независимых неординарных пуассоновских потоков с постоянной характеристикой неординарности l и соответствующими параметром a_l и интенсивностью la_l . Параметр неординарного потока определяется как: ,

а интенсивность такого потока : .

В качестве одного из примеров применения неординарного потока можно привести пуассоновский поток с неординарными заявками, т.е. использующим для своего обслуживания l серверов. В сотовой системе связи в том случае, когда происходит звонок с мобильного телефона на телефоны не расположенные в зоне обслуживания одной базовой станции или на телефоны городской сети, требование обслуживается одним сервером – голосовым каналом, а при осуществлении звонка на мобильный телефон, обслуживаемый одной и той же базовой станцией требуется сразу два сервера – голосовых канала. Следовательно, поток вызовов от мобильных телефонов может рассматриваться как неординарный с характеристикой неординарности равной двум.

Литература

1. Л.Н. Волков, М.С. Немировский, Ю.С. Шинаков. Системы цифровой радиосвязи: базовые методы и характеристики. Учебное пособие.-М.: Эко-трендз, 2005.

2. М.В. Гаранин, В.И. Журавлев, С.В. Кунегин. Системы и сети передачи информации. - М.: Радио и связь, 2001.

3. Н.В. Захарченко, П.Я. Нудельман, В.Г. Кононович. Основы передачи дискретных сообщений. –М.: Радио и связь, 1990.

4. Дж. Прокис. Цифровая связь. - М.: Радио и связь, 2000.

5. Скляр. Цифровая связь. - М.: Радио и связь, 2001.