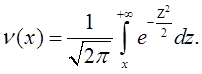Реферат: Достоверность передачи сообщений и надежность систем

,

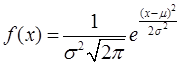Где и - параметры, характеризующие соответственно центр распределения и его масштаб.

Например, при изменении математического ожидания и неизвестном происходит смещение распределения относительно исходного значения (рис. 5), с другой стороны, при изменении среднего квадратичного отклонения и постоянном изменяется форма распределения по вертикали (рис. 6).

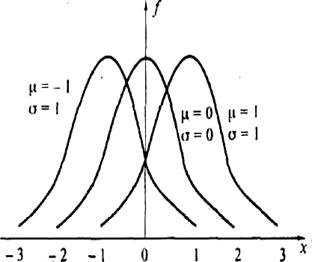
Таким образом, для сигналов с флуктуационной помехой, описываемых выражением ( 4), изменение амплитуды а сигнала означает смещение кривых и по оси U , а изменение влияет на форму распределения по крутизне спада.

С учетом этого нетрудно определить вероятность ошибочного приема символов и пути изменения помехоустойчивости приемника.

Если приемник (см. рис. 4) сравнивает распределения с различным энергию разности между математическим ожиданием сигналами логических 0 и 1 в соответствии с формулами ( 2) и ( 3), то при ее положительном значении фиксируется прием сигнала логической 1, а при отрицательном –

логического 0.

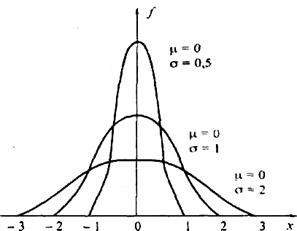
Поэтому при передаче сигнала логического 0 положительные значения напряжения на входе приемника будут приниматься как сигнал логической 1, т.е. будут происходить ошибки , а при передаче сигнала логической 1 отрицатель-

Распределения при изменении иные значения напряжения среднего квадратного отклонения от помех будут фиксироваться как прием сигнала логического 0 (ошибка ). Указанные вероятности ошибок:

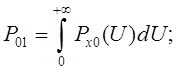
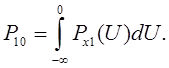
Общая вероятность ошибочного приема символа .

При канал считается симметричным, а приемник — оптимальным по критерию идеального наблюдателя (Зигерта— Котельникова).

Когда потери от ошибок и неравноценны, для приемника выбирают другой критерий — пороговый уровень , перераспределяющий вероятности ошибок.

Действительно, при пороге срабатывания (рис. 7) ошибки:

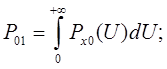( 5)

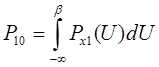. ( 6)

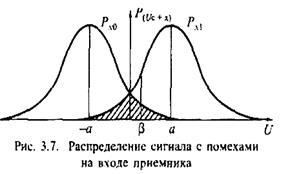
Нетрудно заметить, что сумма подынтегральных площадей при увеличивается, т.е. помехоустойчивость приемника при работе по критерию идеального наблюдателя максимальна.

Выбор оптимального для конкретных условий порога срабатывания является самостоятельной задачей. Например, выбор порога срабатывания по критерию Неймана – Пирсона позволяет при постоянном значении ложного приема минимизировать вероятность пропуска .

Таким образом, помехоустойчивость приемника можно повысить следующими путями:

Увеличением разности энергии сигналов логических 0 и 1, т. е. напряжения а, и, следовательно, раздражением кривых плотностей распределения и ;

изменением формы распределения плотности вероятности сигнала и помехи на входе приемника вследствие повышения удельной энергии сигнала или уменьшения удельной интенсивности помех;

перераспределением вероятности ошибок по ложному приему и пропуску импульсовв результате выбора порогового уровня.

Вероятности ошибок дляреальных приемников рассчитывают по формулам ( 5) и (2.6) с учетом, что подынтегральной функцией является плотность вероятности напряжения U _n на входе приемника, рассчитываемая по формуле ( 1):

.

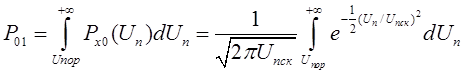Такой интеграл нельзя выразить через элементарные функции. Поэтому его расчетные значения определяются по специальным таблицам вероятностного интеграла: