Реферат: Движение заряженных частиц

Продифференцируем (4) по t и в правую часть уравнения подставим (5).

(6)

Решим уравнение классическим методом: v_y =v_{y пр} +v_{y св} :

Составим два уравнения для определения постоянных интегрирования.

Так как при t=0 v_y =v, то . При t=0 v_z =0. Поэтому или. Отсюда и .

Таким образом,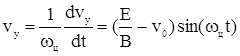

Пути, пройденные электроном по осям у и z:

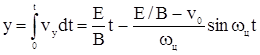
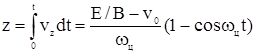
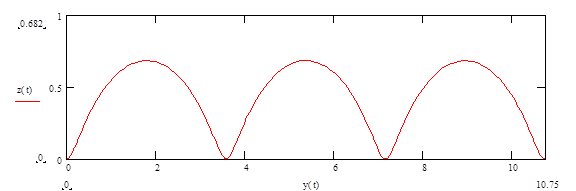
На рис. 6, б, в, г изображены три характерных случая движения при различных значениях v₀ . На рис. 6, б трохоида при v₀ =0, максимальное от­клонение по оси z равно .

Если v₀ >0 и направлена по оси +y, то траекторией является растянутая

трохоида (рис. 6, в) с максимальным отклонением .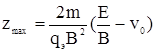

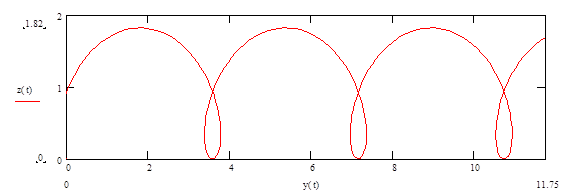
Если v₀ <0 и направлена по оси —у, то траекторией будет сжатая трохоида (рис. 6, г) с .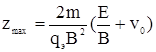

Когда магнитное и электрическое поля мало отличаются от равномерных, траектории движения электронов близки к трохоидам.

??? 6.?

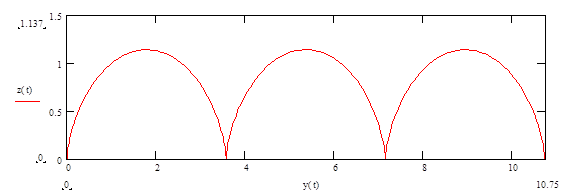Рис 6.в

Рис 6.г

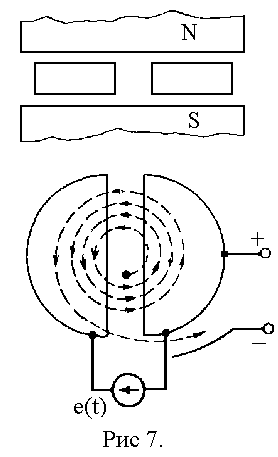
7. Движение заряженных частиц в кольцевых ускорителях.

????????? ???????????? ????? ??? ????? ?????? ? ???? ????????????? ?? ??????????? ????????????????? ?????????. ??? ?????? ????????? ? ??????? ??????????? ?????????? ???? ???????? , ???????????? ?? ???. 7 ?????? ????. ?????? ????????? ? ??????????????? ????? (?? ??????? ?? ???????) ? ???????????? ? ?????????? ?????????? U_m cos(wt). ??? t=0, ????? ?????????? ????? ???????? ????? ???????????? ????????, ? ????????? ????? ?????? ??????????? ?? ????????? ? ??????, ? ???????????? ????? ???????? ?????? ????????????? ????? q. ?? ???? ????? ??????????? ???? . ????? ?????? ????????? ????? ??????? ? ? ????????? ????????? ?????? ? ?????? ??????. ?? ?????? ?????? ?????????????? ?????????????? ???? ????? ????. ???????, ???? ?? ????????? ???. ?? ????? ?? ????????? ????, ?? ????????? ???? , ????????????? ????????? ?????. ??? ????????? ???? ???? ????????????? ?????, ??????????? ?? ????????? v, ????????
???????? ?? ?????????? ???????? . ?????, ? ??????? ???????? ?? ???????? ???-???????,. ???? ??????? ???????????? ????? ???????? ??????????? ????? ?????? , ?? ? ??????? ???????, ????? ????? ?????? ?? ?????? ??????, ?? ???????? ??? ???????????? ?????????????? ????, ?????????????? ?????? ??????. ??? ????????? ????? ???? ????? ??????????? ???? ???????? ? ?????? ? ????? ??????, ??? ????????? ????????? ??????????. ?? ??? ???????? ???????, ??? ??? ????? ???????? ????????. ????? k ???????????? ?????????? ??????? ??????????? ????? ???????? ? ???????, ?????? ??? ????????? ??, ???? ? ?????????? ?????????????? ???? ????????? ?? ????? ???????????, ????????? ??????????? ????? ???????? kU_m . ?? ??? 8. ???????? ???????? ?????????? ?????? ? ??????????.

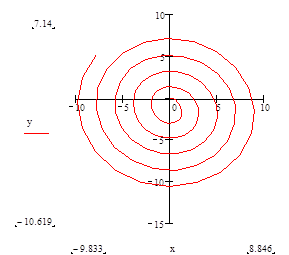Рис 8.

Вывод заряда из циклотрона осуществляется с помощью постоянного электрического поля, созда­ваемого между одной из камер (на рис. 7 пра­вой) и вспомогательным электродом А. С увеличением скорости она становится соизмеримой со скоростью света, масса частицы т во много раз увеличивается. Возрастает и время t₁ , прохождения полуоборота. Поэтому одновременно с увеличением скорости частицы необходимо уменьшать либо частоту источника напряжения U_m cos(wt) (фазотрон), либо величину индукции магнитного поля (синхротрон), либо частоту и индукцию (синхрофазотрон).