Реферат: Экономико-статистический анализ производства молока в ЗАО Оглухинское Крутинского района

Простая применяется в тех случаях, когда имеются значения признаков по каждой единице совокупности или когда каждое значение признака встречается в совокупности одинаковое число раз.

Значения изучаемого признака называются вариантами и обозначаются , а средняя величина - .

Средняя арифметическая взвешенная исчисляется, когда значение признака (варианты) встречаются в совокупности неодинаковое число раз.

Средняя гармоническая представляет собой обратную величину средней арифметической из обратных величин. Бывает простая и взвешенная .

Средняя гармоническая применяется, если имеются данные об индивидуальных значениях признака и общем объеме совокупности, но не известны частоты.

Средняя хронологическая применяется в тех случаях, когда необходимо рассчитать средний уровень моментного ряда динамики.

Средняя геометрическая применяется для расчета среднегодового темпа роста в рядах динамики.

В некоторых случаях исчисляются специфические показатели, которые называются средние структурные:

Мода - наиболее часто встречающееся значение признака в совокупности, т. е. варианта с наибольшей частотой.

Медиана - варианта, расположенная в середине вариационного ряда.

Рассматривая зарегистрированные в процессе наблюдения значения какого - либо признака об отдельных единицах совокупности, можно обнаружить между ними различия.

Колеблемость, изменяемость величины признака у единиц совокупности называется вариацией.

Вариация измеряется с помощью следующих показателей:

1.Размах вариации: , (22)

где - максимальное и минимальное значения признака

2.Среднее линейное отклонение : (23)

3. Дисперсия – средний квадрат отклонений индивидуальных значений признака от средних значений.

D=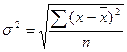- для несгруппированных данных (24)

D=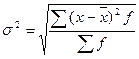 - для сгруппированных данных (25)

4. Среднее квадратическое отклонение:

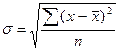(26)

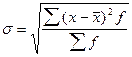(27)

Коэффициент вариации показывает относительную степень изменчивости (вариации) в ряду распределения:

(28)

Расчеты величин удобно представить с помощью вспомогательных расчетных таблиц. Расчеты будем производить для качественного показателя- удоя молока от одной коровы.

Таблица 5

Расчет величин для определения показателей вариации удоя молока от одной коровы в ЗАО «Оглухинское» Крутинского района Омской области за 2005 год

Предприятия	Среднегодовой удой молока от1 коровы, ц	Среднегодовое поголовье коров, голов	Валовой удой молока, ц	Отклонение фактического от среднего значения	Произведение отклонения на частоту	Произведение квадрата отклонения на частоту	Накопленные частоты
	х	f	xf=X		f	(x-)2 f	S
ЗАО Новопокровское	5,00	28	140	26,68	747,04	19931,03	-
ЗАО Крутинское	14,27	79	1127	17,41	1375,39	23945,54	2696
ЗАО Рыжковский	14,51	130	1886	17,17	2232,1	38325,16	2668
СПК Красноярский	14,91	108	1610	16,77	1811,16	30373,15	1230
СПК Ировский	17,05	59	1006	14,63	863,17	12628,18	4237
ЗАО Шипуновское	17,50	308	5390	14,18	4367,44	61930,30	1289
СПК Ингалинский	20,01	218	4362	11,67	2544,06	29689,18	4545
СПК Евгащинский	26,49	1098	29086	8,19	8992,62	73649,56	4129
СПК Восход	27,86	117	3260	3,82	446,94	1707,31	3911
ЗАО Оглухинское	3483	1100	38313	3,15	3465	10914,75	2813
ЗАО им. Кирова	44,45	1300	57785	12,77	16601	211994,77	1100
Итого	X	4545	143965	146,14	43445,92	515088,93

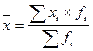- среднее значение удоя молока от одной коровы рассчитаем по формуле средней арифметической взвешенной

143965/4545=31,68 ц

Модальное значение признака равно 44,45 ц, т.к. по определению мода- это варианта, имеющая наибольшую частоту.

Для того чтобы найти медианное значение удоя молока, нужно сначала проранжировать предприятия по удою молока с 1 коровы, потом найти такую накопленную частоту, которая будет превышать половину совокупности.

n=4545 голов

=4545/2=2272,5 голов

Первая накопленная частота, превышающая половину совокупности , равна 3245, что соответствует среднегодовому удою молока от одной коровы в размере 34,83 ц. молока, поэтому медиана равна 34,83 ц.

43445,92/4545=9,56 ц (23)

=515088,93/4545=113,34 (25)

- среднее квадратическое отклонение

ц (27)

=10,65/31,68*100%=33,62% (28)

R=44,45-5=39,45ц (22)

По представленным показателям вариации можно сделать следующие выводы.

Рассчитав среднюю величину ряда, получили ее равную 31,68 ц молока, это означает, что такое количество молока дает одна корова в среднем. Чаще всего встречающее значение удоя молока с одной коровы равно 44,45 центнеров. Половина предприятий в изученной совокупности имеет меньше 1100 голов, а вторая половина больше. Среднее квадратическое отклонение показывает, что каждое индивидуальное значение вариации среднегодового удоя молока отклоняется от среднего значения, равного 31,68 ц, в пределах от 9,56 до 10,65 ц. в среднем, что в относительных единицах составляет 33,62 %, это означает, что совокупность признается неоднородной, а средняя величина – нетипической для данной совокупности. Разница между граничными значениями удоя молока от одной коровы равна 39,45 Ц.