Реферат: Електромагнітний витратомір для трубопроводів великих діаметрів

Публікації. За результатами досліджень, виконаних в дисертації, опубліковано 12 наукових праць, 5 з них опубліковані в фахових періодичних наукових журналах, 5 робіт опубліковані в збірниках наукових праць міжнародних та українських конференцій і 2 роботи – в тезах українських конференцій з метрології.

Структура дисертації . Дисертація складається із вступу, чотирьох розділів, висновку, списку використаних джерел та додатків. Повний обсяг дисертації налічує 173 сторінки, де 19 малюнків, 11 таблиць та 5 додатків. Список використаних джерел має 127 найменувань.

ОСНОВНИЙ ЗМІСТ РОБОТИ

У вступі дано коротку характеристику дисертаційної роботи: обгрунтовано актуальність теми; сформульовано цілі і задачі дослідження; визначено наукову новизну і практичну цінність роботи; викладено основні положення, що виносяться на захист; визначено авторський внесок у сумісних роботах, а також наведено відомості про апробацію результатів виконаних досліджень.

У першому розділі наведено результати аналітичного огляду сучасного стану методів та засобів вимірювальної техніки для вимірювання об'ємної витрати рідинних потоків у трубопроводах великих діаметрів.

Показано, що поставленому завданню щодо створення ЗВТвитрати рідинних середовищ у заповнених трубопроводах у найбільшіймірі відповідає електромагнітний метод, що дозволяє створювати прилади з високими метрологічними й експлуатаційними характеристиками, надійністю, стабільністю показів, можливістю їх використання в автономному режимі і передачі інформації на великі відстані без втрат і спотворень. Проте засоби вимірювальної техніки для трубопроводів великих діаметрів не можуть копіювати традиційні електромагнітні витратоміри для трубопроводів малих діаметрів, де магнітні системи охоплюють трубу подібно системі відхилення кінескопа, оскільки в цьому разі на діаметрах 1000 мм і більше їх вага складатиме декілька тисяч кілограмів, тобто вони мають великі габарити, металоємність і енерговитрату і тому практично не застосовуються для вимірювання витрати рідини у трубопроводах великих діаметрів. Водночас, з огляду на достоїнства електромагнітного методу, дуже перспективним є створення компактних ЕМВ змалою металоємністюна основі МГД ЛМП, які мають низьку енерговитрату, невелику вартість, зручність в експлуатації та забезпечують вимірювання витрати у заповнених трубопроводах великих діаметрів за методом “площа-швидкість”, заснованим на визначенні об'ємної витрати рідини за швидкістю потоку в одній точці (точці середньої швидкості) поперечного перетину трубопроводу і площіостаннього, відповідно до ISO 7145 і ГОСТ 8. 361-79. Однак до цього дня такі ЗВТ були недостатньо вивчені.

На підставі проведеного детального аналізу визначено мету і поставлено задачі, які вирішуються в наступних розділах.

В другому розділі проведено теоретичні дослідження найбільш перспективного на цей час витратоміра з циліндричним МГД ЛМП на основі розв'язання системи рівнянь магнітної гідродинаміки при відповідних граничних умовах (оскільки сигнал таких ЗВТ формується в потоці рідини, що рухається в його магнітному полі), яка складається з рівнянь Максвеллаі рівнянь гідродинаміки (рівняння нерозривності і рівняння руху) для в'язкої нестисливої провідної рідини

Показано, що теорію роботи МГД ЛМП до теперішнього часу було розглянуто в недостатній мірі. Це обумовлено тим, що теоретичні дослідження пов'язані з математичними труднощами опису магнітогідродинамічних процесів у робочій області таких перетворювачів. Задача ускладнюється ще й тим, що шукане рішення повинно бути у високому ступені адекватним процесам, які відбуваються в робочій області МГД ЛМП, а саме індукованаЕРС (сигнал ЕМВ) повинна визначатися тільки швидкістю прямування рідини в “точці” виміру – точці середньої швидкості і не залежати, відповідно до ISO 7145 і ГОСТ 8.361-79, від епюри швидкостей і її градієнтів у трубопроводі, тобто питання стосується обліку "тонких" моментів – впливу розподілу швидкості вимірюваного потоку та її градієнтів на покази МГД ЛМП.

Розглянуто математичну модель МГД ЛМП і показано, що сигнал таких ЗВТ – різниця потенціалів на вимірювальних електродах перетворювача, що контактують із досліджуваним потоком (рис.1), визначається розподілом індукованих струмів у вимірюваному середовищі

Сформульовано задачу синтезу МГД ЛМП, яка дозволяє визначити їх оптимальні параметри та полягає у визначенні розподілу індукованих струмів j (електричного потенціалу j ) у робочій областіперетворювача, обтічного потоком V в'язкого нестисливого провідного середовища на основі розв'язання системи двох задач Неймана для рівнянь Пуансона і Лапласа для електричного та магнітного потенціалів відповідно:

Показано, що при цьому розподіл швидкостей у вимірюваному потоці рідини визначається системою рівнянь класичної гідродинаміки.

Для дослідження питання щодо ступеня залежності показів МГД ЛМП від поперечного градієнта швидкості, яке на сьогодні лишається відкритим і потребує відповіді, розглянуто і вирішено задачу про формування сигналу МГД ЛМП, встановленого в трубопроводі радіуса R та обтічного турбулентним потоком нестисливої провідної рідини (рис.2), де Е 1(r , 0,758R , 0) та Е 2(-r , 0,758R , 0) – розташовані у точках середньої швидкості електроди МГД ЛМП.

На основі отриманого рішення цієї задачі визначено сигнал МГД ЛМП при його використанні як ЕМВ у трубопроводах великих діаметрів при довільному розподілі магнітної індукції та поля швидкостей

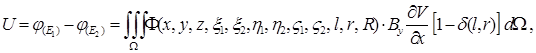(4)

де - приріст функції Гріна на електродах МГД ЛМП, - функція Гріна абофункція впливу у задачіНеймана для рівняння Пуассона (3) в областіW - внутрішності трубопроводу радіуса R із вставленим у нього циліндричним перетворювачем радіуса r довжиною 2l (рис.1), x , h , V - відповідна x , y , z декартова система поточних координат.

Отже, доданок d (l , r )

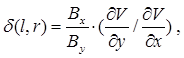(5)

обумовлений геометричними та конструктивними параметрами МГД ЛМП та градієнтом швидкості потоку, і визначає ступінь залежності його показів від характеристик потоку.

Проведено ретельний аналіз величиниd (l , r ) з метою її мінімізації, тобто мінімізації залежності показів розроблюваного ЕМВ від структури потоку, що вимірюється.

За умови використання МГД ЛМП у трубопроводах великих діаметрів та згідно з ГОСТ 8.361 при вимірюванні розвинених турбулентних течій епюру швидкостей у трубопроводі задано у вигляді

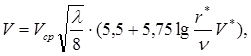(6)

деl = 0,0032+0,221ЧRe-0 ,237 – коефіцієнт опору трубопроводу, визначений універсальним співвідношенням у формі Никурадзе; n - кінематичний коефіцієнт в'язкості вимірюваного середовища; - відстань від осі трубопроводу до аналізованоїточки; 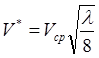- динамічна швидкість – величина, обумовлена тертям на стінці і густиною рідини.

Експериментально визначено значення магнітної індукції на межі z = ± l (рис.1), що дозволило отримати аналітичний вираз, який з достатньою точністю (похибка ~ 1%) описує розподіл магнітного поля розсіяння МГД ЛМП у вимірюваному середовищі в залежності від параметрів магнітної системи перетворювача. Це співвідношення є основоположним при розробці МГД ЛМП.

Отримано аналітичний вираз, який визначає характер та ступінь впливу структури вимірюваного потоку на покази МГД ЛМП:

На основі аналізу одержаного виразу (7) синтезовано МГД ЛМП з високими метрологічними характеристиками для трубопроводів великих діаметрів.

У третьому розділі розглянуто питання синтезу МГД ЛМП – питання визначення їх оптимальних параметрів, при яких такі ЗВТ забезпечували б вимірювання витрати у трубопроводах великих діаметрів з нормованими метрологічними характеристиками.

Розглянуто основні фактори, які впливають на метрологічні характеристики МГД ЛМП. Це – завантаження вимірювального перетину трубопроводу перетворювачем та поперечний градієнт швидкості.

Розрахунок оптимальних параметрів r та l (рис.1) котушки збудження магнітного поля МГД ЛМП, при яких d (l , r ) << 1 (5,7), за рахунок чого залежність показів таких перетворювачів від поперечного градієнта швидкості (4) буде зведено до придатного мінімуму, виконано згідно з отриманим у другому розділі рішенням задачі синтезу (4,7) для різних значень r та l . Встановлено, що оптимальним є відношення l /r = 0,5 та r Ј 32 мм при D у і 300 мм. При цьому похибка вимірювання витрати буде знаходитися на рівні ± 1,0 %.