Реферат: Электрооптические модуляторы света
где R - коэффициент отражения зеркал, а φ - фазовый сдвиг света при прохождении через среду, определяемый следующим образом:
![]() (5)
(5)
здесь L - толщина пластинки. Показатель преломления n при наличии внешнего электрического поля записывается в виде
![]() (6)
(6)

Рис.3. Электрооптический модулятор Фабри-Перо.
Подставляя выражение (6) для n в (5), получаем
![]() (7)
(7)
где V - приложенное напряжение.
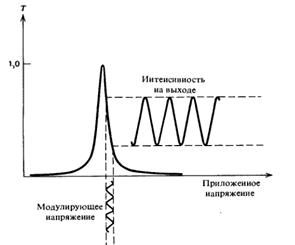
Рис.4. Зависимость коэффициента пропускания электрооптического модулятора Фабри-Перо от приложенного напряжения.
Модулятор смещен в рабочую точку, расположенную на полувысоте максимума пропускания. Небольшое приложенное синусоидальное напряжение приводит к модуляции интенсивности на выходе относительно точки смещения. Если падающий световой пучок является монохроматическим, то интенсивность прошедшего пучка зависит от величины φ, которая, как следует из (7), является электрически перестраиваемой. Кроме того, если резонатор Фабри-Перо смещен таким образом, что коэффициент его пропускания в отсутствие модулирующего напряжения равен 50%, то интенсивность прошедшего излучения будет сильно модулироваться относительно малыми модулирующими напряжениями. Это иллюстрируется на рис.4. Большая глубина модуляции обусловлена резким пиком пропускания, разумеется, при условии, что резонатор имеет высокую добротность. Действительно, в соответствии с выражением (4) наклон кривой пропускания в точке, расположенной на ее полувысоте, запишется в виде
![]() (8)
(8)
где F - добротность резонатора. Нетрудно изготовить резонаторы Фабри-Перо с добротностью F = 30. Таким образом, наклон кривой пропускания, определяемый выражением (8), может быть порядка 10. В обычных амплитудных модуляторах этот наклон равен 1. Пусть приложенное напряжение имеет вид V = Vm sinωm t.
Световой пучок, прошедший через модулятор, приобретает фазовый множитель е- ikL , который содержит фазу, отвечающую нулевому полю (Е = 0), и электрически индуцированное изменение фазы вычисляется по формуле:
![]() (9)
(9)
где V - приложенное напряжение. Напряжение, требуемое для изменения фазы на π, называется полуволновым напряжением фазовой модуляции и дается выражением
![]() (10)
(10)
Тогда глубину модуляции прошедшего пучка с помощью выражений (8), (9) и (10) можно записать в виде
![]() (11)
(11)
Заметим, что по сравнению с выражением (3) здесь при том же напряжении ![]() глубина модуляции увеличивается в F/π раз.
глубина модуляции увеличивается в F/π раз.
Фазовая модуляция
Хотя амплитудно-модулированный свет после прохождения через электрооптический модулятор Фабри-Перо оказывается промодулированным также и по фазе, имеется необходимость в получении светового пучка с чисто фазовой модуляцией.
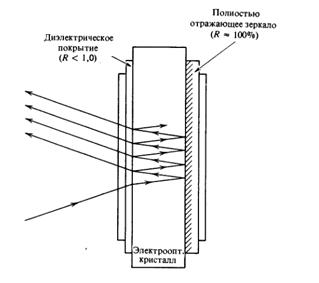
Рис.5. Работа асимметричного реюнатора Фабри - Перо (эталона Жира-Турнуа) в качестве фазового модулятора.
Идеализированная структура чисто фазового модулятора изображена на рис.5.
Он представляет собой асимметричный резонатор Фабри-Перо, заднее зеркало которого имеет коэффициент отражения 100%. Переднее зеркало имеет частично отражающее диэлектрическое покрытие с R < 1,0. Это так называемый эталон Жира-Турнуа.
Коэффициент отражения полной структуры, очевидно, равен 100%, поскольку свет не может проходить через второе зеркало и полная структура не имеет потерь.
Если в спектральном диапазоне, представляющем интерес, коэффициент отражения зеркала сохраняется равным 100%, то будет отражаться вся электромагнитная энергия. Действительно, коэффициент отражения можно записать в виде