Реферат: Елементи дисперсійного аналізу і теорії кореляції

(8)

– рівняння регресії на .

Аналогічно визначаються умовне математичне сподівання випадкової величини і функція, а також рівняння регресії на :

(9)

Функції і (рівняння регресії), що уявляють інтерес, у загальному випадку невідомі, тому їх шукають у наближеному вигляді, причому звичайно обмежуються лінійним наближенням:

(10)

де і – параметри, що підлягають визначенню. Найчастіше для цього вживають метод найменших квадратів.

Функцію називають "найкращим наближенням" у сенсі методу найменших квадратів, якщо математичне сподівання

(11)

приймає найменше можливе значення. При цьому функцію називають середньоквадратичною регресією на .

У теорії ймовірностей доведено, що лінійна середня квадратична регресія на має вигляд

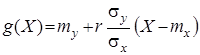
де

, ,

, ,

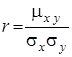– коефіцієнт кореляції величин і ,

– кореляційний момент цих величин.

Можна показати, що кореляційний момент характеризує зв'язок між величинами і , зокрема, якщо вони незалежні, то

Коефіцієнт

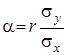
називають коефіцієнтом регресії на , а пряму

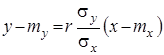(12)

називають прямою середньоквадратичної регресії на .

При підстановці знайдених значень і у формулу (11) отримуємо мінімальне значення функції , що дорівнює

Цю величину називають залишковою дисперсією випадкової величини щодо випадкової величини . Вона характеризує похибку, що виникає під час заміни лінійною функцією (10). При залишкова дисперсія дорівнює нулю, тобто в цих випадках лінійна функція (10) точно подає випадкову величину . Це означає, що при цьому та пов'язані лінійною функціональною залежністю.

Аналогічний вигляд має і пряма середньоквадратичної регресії на

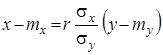(13)