Реферат: Элементы физики ядра

β–излучение

Отклоняется электрическим и магнитным полями; его ионизирующая способность значительно меньше (примерно на два порядка), а прони­кающая способность гораздо больше, чем у α–частиц. Представляет собой поток быстрых электронов.

γ–излучение

Не отклоняется электрическим и магнитным полями, обладает относи­тельно слабой ионизирующей способностью и очень большой проникаю­щей способностью, при прохождении через кристаллы обнаруживает дифракцию. Представляет собой коротковолновое электромагнитное излучение с чрезвычайно малой длиной волны м и вследствие этого – ярко выраженными корпускулярными свойствами, т. е. явля­ется потоком частиц – γ-квантов (фотонов).

Рис. 12.4

Закон радиоактивного распада

Закон самопроизвольного радиоактивного распада основывается на двух предположениях:

1) постоянная распада не зависит от внешних условий;

2) число ядер, распадающихся за время dt, пропорционально наличному количеству ядер.

Эти предположения означают, что радиоактивный распад является статистическим процессом и распад данного ядра является случайным событием, имеющим вероятностный характер.

Предположим, что в момент времени t было N радиоактивных ядер,

а в момент времени t + dt осталось N – dN нераспавшихся ядер.

Убыль числа ядер за время определяется как: .

Можно считать, что число ядер, распадающихся за время , пропорционально N и :

,

где – постоянная распада . Интегрирование этого равенства дает

– основной закон радиоактивного распада.

Формулировка основного закона радиоактивного распада :

число еще нераспавшихся ядер N убывает со временем по экспоненте

(см. рис. 12.5). Здесь N – число нераспавшихся ядер к моменту времени t ; – начальное число не­распавшихся ядер (в момент времени ).

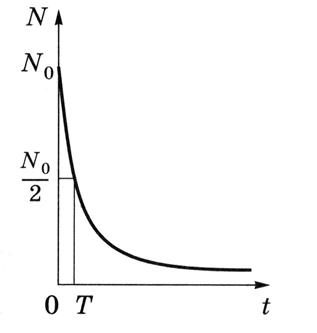
Рис. 12.5

Интенсивность радиоактивного распада характеризуют чис­лом ядер, распадающихся в единицу времени . Ее называют активностью А. Таким образом, активность

.

Ее измеряют в беккерелях (Бк), 1 Бк = 1 распад/с; а также в кюри (Ки), 1 Ки = 3.7 Бк.

Период полураспада

Период полураспада – промежуток времени, за который в среднем число нераспавшихся ядер уменьшается вдвое (см. рис. 12.5).

Подставляя в формулу, выражающуюосновной закон радиоактивного распада, получим:

.

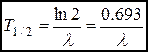Для известных в настоящее время радиоактивных ядер варьируется от с до лет.

Среднее время жизни радиоактивного ядра

Количество ядер, распавшихся за промежуток времени (t , ), равно

.

Время жизни каждого из ядер равно t . Следовательно, сумма времен жизни всех имевшихся первоначально ядер определяется интегрированием выражения по времени от 0 до . Разделив сумму времен жизни всех ядер на , получим среднее время жизни τ ядра:

.

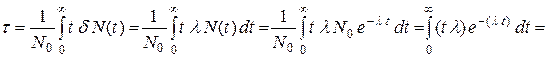
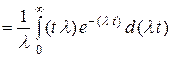Для выполнения интегрирования перейдем к новой переменной . Интегрирование выполним по частям: 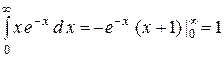. Таким образом, получим

.
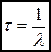