Реферат: Энтропия сложных сообщений, избыточность источника. Цель сжатия данных и типы систем сжатия

Энтропия сложных сообщений, избыточность источника

Рассмотренные выше характеристики источника - количество информации и энтропия - относились к одному источнику, вырабатывающему поток независимых или простых сообщений, или к источнику без памяти.

Однако в реальных условиях независимость элементарных сообщений, вырабатываемых источником, - явление довольно редкое. Чаще бывает как раз обратное - сильная детерминированная или статистическая связь между элементами сообщения одного или нескольких источников.

Например, при передаче текста вероятности появления отдельных букв зависят от того, какие буквы им предшествовали. Для русского текста, например, если передана буква "П ", вероятность того, что следующей будет "А ", гораздо выше, чем "Н ", после буквы "Ъ " никогда не встречается "H " и т.д. Подобная же картина наблюдается при передаче изображений - соседние элементы изображения имеют обычно почти одинаковые яркость и цвет.

При передаче и хранении данных часто также имеют дело с несколькими источниками, формирующими статистически связанные друг с другом сообщения. Сообщения, вырабатываемые такими источниками, называются сложными сообщениями , а сами источники - источниками с памятью .

Очевидно, что при определении энтропии и количества информации в сообщениях, элементы которых статистически связаны, нельзя ограничиваться только безусловными вероятностями - необходимо обязательно учитывать также условные вероятности появления отдельных сообщений.

Определим энтропию сложного сообщения, вырабатываемого двумя зависимыми источниками (подобным же образом определяется энтропия сложного сообщения, вырабатываемого одним источником с памятью).

Пусть сообщения первого источника принимают значения x₁ , x₂ , x₃ ,....x_k с вероятностями, соответственно, P(x₁ ), P(x₂ ),..... P(x_k ), сообщения второго - y₁ , y₂ ,.....y_m с вероятностями P(y₁ ), P(y₂ ),..... P(y_m ).

Совместную энтропию двух источников X и Y можно определить следующим образом:

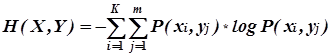, (1)

где P(x_i ,y_j ) - вероятность совместного появления сообщений x_i и y_j . Поскольку совместная вероятность P(x_i ,y_j ) по формуле Байеса определяется как

, (2)

то выражение для совместной энтропии можно записать в следующем виде:

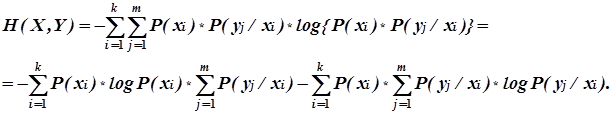(3)

Так как передаче сообщения x_i обязательно соответствует передача одного из сообщений (любого) из ансамбля Y , то

(4)

и совместная энтропия H(X,Y) определится как

, (5)

где H ( Y/x_i ) - так называемая частная условная энтропия, отражающая энтропию сообщения Y при условии, что имело место сообщение x_i . Второе слагаемое в последнем выражении представляет собой усреднение H ( Y/x_i ) по всем сообщениям x_i и называется средней условной энтропией источника Y при условии передачи сообщения X . И окончательно:

H (X,Y ) = H (X) + H (Y/X) . (6)

Таким образом, совместная энтропия двух сообщений равна сумме безусловной энтропии одного из них и условной энтропии второго .

Можно отметить следующие основные свойства энтропии сложных сообщений:

1. При статистически независимых сообщениях X и Y совместная энтропия равна сумме энтропий каждого из источников:

H (X,Y) = H (X) + H (Y) , (7)

так как H (Y/X) = H (Y).

2. При полной статистической зависимости сообщений X и Y совместная энтропия равна безусловной энтропии одного из сообщений. Второе сообщение при этом информации не добавляет. Действительно, при полной статистической зависимости сообщений условные вероятности P(y_j /x_i ) и P(x_i /y j) равны или нулю, или 1, тогда

P(x_i /y_j )*log P(x_i /y_j ) = P(y_j /x_i )*log P(y_j /x_i ) = 0 (8)

и, следовательно, H (X,Y) = H (X) = H (Y).

3. Условная энтропия изменяется в пределах

--> ЧИТАТЬ ПОЛНОСТЬЮ <--