Реферат: Эпюр как инструмент исследования потребительского поведения
Если сейчас я сразу же изображу проекции рисунка 1 на эпюре, последующие построения и выводы не для каждого читателя будут понятными. Поэтому в данном случае следует использовать процедуру изучения проблемы по принципу <от простого к сложному>.
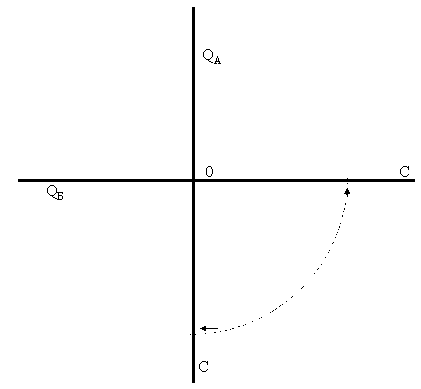
Рисунок 3. Разворот на плоскость пространства "доход потребителя - объем товара А - объем товара Б" (первый этап построения эпюра)
Самый простой случай в данной ситуации - когда указанные две проекции на плоскости <объемы-доход> одинаковы. Я уже указывал выше на то, что этот случай маловероятен, тем не менее удобнее всего начинать именно с него. Действительно, одному и тому же значению дохода соответствует одно и то же значение объема как на проекции в первом квадранте, так и на проекции в третьем квадранте. Это, в свою очередь, означает, что на проекции кривой во втором квадранте, координаты которого определяются значениями двух объемов, каждая точка проекции будет характеризоваться координатами, равными друг другу. Товар А начинает потребляться при том же доходе, что и товар Б; объемы максимального потребления товара А равны объему максимального потребления товара Б при одной и той же величине дохода; объемы рационального потребления у них также равны друг другу и тому подобное. По сути, во втором квадранте будет получено множество пар точек, координаты которых равны, например, (2;2), (5;5), (10;10) и т.п.
Таким образом, проекция кривой на плоскость "объем товара А - объем товара Б" будет представлять собой отрезок прямой линии, выходящий из начала координат под углом в 45 градусов. Причем, с ростом дохода линия начнет увеличиваться от нулевой точки к точке максимального значения, а затем, по той же самой траектории вернется в точку, координаты которой равны рациональным объемам потребления.

Рисунок 4. Эпюр кривой совместного распределения товаров (невероятный случай)
Описанный эпюр представлен на графике рисунка 4. На нем пунктиром показано построение наиболее характерных точек проекции кривой на плоскость объемов. Точка, обозначенная словом "max" характеризует максимальные значения объемов. Первоначальный участок кривой находится между нулевой точкой (начало координат) и этой точкой. С дальнейшим увеличением дохода проекция кривой на плоскость объемов будет представлена отрезком от точки "max" до точки "rat", которая характеризует рациональный объем потребления.
Очевидно, что рассмотренный случай является невероятным. Конечно же, в реальной жизни равновесные кривые, а значит, и их проекции никогда не совпадут полностью во всех точках. Будет пусть небольшое, но все же расхождение точек. Значит, проекция такой кривой на плоскость объемов уже будет иметь нелинейную форму. Чем больше расхождение в проекциях кривых на плоскости доход - объемы товаров, тем в большей степени совместная кривая распределения объемов будет нелинейной.
Пусть для определенности проекция равновесной кривой товара А на плоскость объем-доход имеет первоначальный объем, начинающийся из нулевой точки. Некоторая часть участка кривой совместного распределения товаров в пространстве будет лежать на плоскости объем товара А - доход. Действительно, до достижения некоторой величины дохода объемы потребления товара Б являются нулевыми. На проекции рассматриваемой кривой на плоскость объемов этот участок кривой будет изображен отрезком прямой, совпадающим с осью объемов товара А.
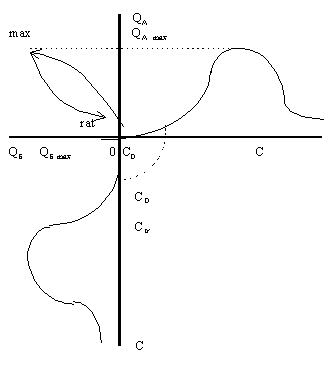
Рисунок 5. Эпюр кривой совместного распределения товаров и проекция на плоскость объемов
Значит, в отличие от графика рисунка 4, на котором проекция полностью сливается с отрезком прямой, выходящим из начала координат, данная кривая начнется из точки, лежащей выше начала координат на оси объемов товара А (рисунок5). На рисунке показано, что для получения этой точки необходимо на оси доходов найти такую его величину, при которой начнется приобретение товара Б. При этом товар А уже потребляется в некотором объеме. Точка с этим объемом на оси QА и есть точка начала проекции кривой на плоскость объемов. В отличие от предыдущего случая проекция уже не является линейной. Участок проекции до максимальной точки и после нее является нелинейным, хотя кривизна в этом случае незначительная.
Предположу теперь, что проекция равновесной кривой товара А на плоскость объем-доход отличается от проекции товара Б не только тем, что его потребление начинается раньше, но и тем, что максимальный объем у этой кривой выше, а доход, при котором проекция достигает этого максимума, сдвинут на оси доходов левее. Пусть при этом и объем рационального потребления данного товара меньше, чем объем рационального потребления товара Б (рисунок6).
В этом случае проекция совместного распределения товаров на плоскость объемов будет иметь очень интересный нелинейный характер.
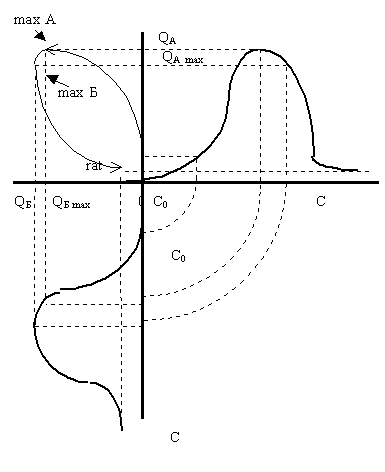
Рисунок 6. Эпюр кривой совместного распределения товаров и проекция на плоскость объемов
Действительно, начнется эта кривая из той же точки, что и кривая, изображенная на предыдущем рисунке (рисунок 5). Затем, кривая будет стремиться к максимуму объема товара А, так как он наступает при более ранних значениях дохода. При достижении этого максимума, объем товара А постепенно начнет уменьшаться, а объем товара Б будет продолжать еще некоторое время увеличиваться - проекция кривой совместного распределения объемов двух товаров при этом движется влево и вниз.
После того, как доход потребителя достигнет величины, при которой товар Б приобретается в максимальных объемах, с дальнейшим увеличением дохода начнут уменьшаться объемы и товара А, и товара Б. Кривая совместного распределения при этом направится вправо вниз вплоть до точки рациональных объемов.
В данном случае, который вполне можно признать вероятным, получилась оригинального вида петля, как траектория совместного распределения товаров в зависимости от доходов.
Очевидно, что совместное распределение товаров на плоскости объемов может иметь и другие формы в зависимости от того, каково соотношение между наиболее характерными точками проекций равновесных кривых на плоскости объем-доход.
В частности, возможна очень интересная форма петли, которая изображена на рисунке 7. В этом случае товар А с увеличением доходов начинает потребляться раньше, чем товар Б, но товар Б покупается интенсивнее, и максимум его потребления наступает раньше. При насыщении рынка двумя товарами объем рационального потребления товара Б больше, чем товара А.
Читатель может самостоятельно построить эпюр данной кривой и осуществить построение кривой распределения объемов товаров, как одну из проекций трехмерной кривой. Для того, чтобы не загромождать книгу излишними построениями, я не привожу здесь это построение, а показываю лишь полученный результат (рисунок 7).
В результате получена очень красивой формы петля совместного распределения объемов двух товаров, которая, как видно из рассуждений, предваряющих ее построение, вовсе не является чем-то невероятным. Более того, появление таких петель в экономической практике следует считать вполне заурядным явлением.
Очень интересным в данной петле является то, что она пересекает сама себя. Одной и той же точке на плоскости объемов при этом соответствуют разные значения дохода, отражаемые данной кривой, что, как будет показано ниже, противоречит постулатам классической теории потребительского поведения (в частности, гипотезе о ненасыщаемости). Следует отметить, что кривая на плоскости - проекция трехмерной кривой, и такие пересечения проекций являются вещами обыденными в начертательной геометрии.

Рисунок 7. Одна из возможных петель распределения товаров.
Не буду утомлять читателя другими геометрическими построениями, скажу лишь, что мне удавалось получить петли, имеющие форму восьмерки. И вновь такая форма не является чем-либо исключительным в экономической практике.
Подводя итог данному параграфу, следует заметить, что кривые совместного распределения имеют самые различные формы, но в подавляющем большинстве случаев эта форма имеет простой петлеобразный характер.