Реферат: Физические основы электроники

Так как через изолированный полупроводник ток про­ходить не должен, между диффузионным и дрейфовым то­ками устанавливается динамическое равновесие:

. (1.15)

Приконтактную область, где имеется собственное электрическое поле, называют p- n переходом .

Поскольку потенциальная энергия электрона и потен­циал связаны соотношением W = -qU, образование не­скомпенсированных объемных зарядов вызывает пониже­ние энергетических уровней n-области и повышение энер­гетических уровней р-области. Смещение энергетических диаграмм прекратится, когда уровни Ферми W _{ф n} и W _{ф p} совпадут (рис. 1.7, д). При этом на границе раздела (x = 0) уровень Ферми проходит через середину запрещенной зоны. Это означает, что в плоскости сечения x = 0 полупровод­ник характеризуется собственной электропроводностью и обладает по сравнению с остальным объемом повышен­ным сопротивлением. В связи с этим его называют запи­рающим слоем или областью объемного заряда.

Совпадение уровней Ферми n- и p-областей соответству­ет установлению динамического равновесия между облас­тями и возникновению между ними потенциального барь­ера U_k для диффузионного перемещения через p-n переход электронов n-области и дырок p-области.

Из рис. 1.7, д следует, что потенциальный барьер

.

Подстановка в это выражение результатов логарифмиро­вания соотношений (1.4), (1.7) позволяет получить сле­дующее равенство:

.

Если обозначить j_т = kT/q и учесть уравнение (1.10), то можно записать:

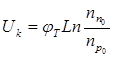; (1.16) 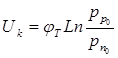. (1.17)

Из уравнений (1.16) и (1.17) следует:

; . (1.18)

При комнатной температуре (Т = 300 К) j_т » 0,026 В.

Таким образом, контактная разность потенциалов зави­сит от отношения концентраций носителей зарядов одного знака в р- и n-областях полупроводника.

Другим важным параметром p-n перехода является его ширина, обозначаемая d = d_p + d_n .

Ширину запирающего слоя d можно найти, решив урав­нения Пуассона для n-области и p-области:

; (1.19) . (1.20)

Решения уравнений (1.19) и (1.20) при граничных ус­ловиях

; ;

имеют вид:

для -d_p < x < 0;

для 0 < x <d_n ; (1.21)

В точке x = 0 оба решения должны давать одинаковые значения j и . Приравняв и , можно записать:

. (1.22)

Из равенства (1.22) видно, что ширина слоев объемных зарядов в n- и p-областях обратно пропорциональна кон­центрациям примесей и в несимметричном переходе запи­рающий слой расширяется в область с меньшей концен­трацией примесей.

На основании равенства (1.22) можно записать:

; , (1.23)

где d = d_n + d_р .

Приравнивая правые части уравнений (1.21) и учиты­вая соотношения (1.23), при x = 0 получаем

.

На основании этого выражения формулу для определения ширины запирающего слоя p-n перехода можно записать в следующем виде:

. (1.24)

Из соотношения (1.24) видно, что на ширину запираю­щего слоя существенное влияние оказывает концентрация примесных атомов. Увеличение концентрации примесных атомов сужает запирающий слой, а уменьшение расширя­ет его. Это часто используется для придания полупровод­никовым приборам требуемых свойств.

1.3.2 Прямое включение p- n перехода

При использовании p-n перехода в полупроводниковых приборах к нему подключается внешнее напряжение. Ве­личина и полярность этого внешнего напряжения опреде­ляют электрический ток, проходящий через p-n переход.

Если положительный полюс источника питания подклю­чается к

р-области, а отрицательный полюс - к n-обла?