Реферат: Физико-химические свойства нефтей

Одной из наиболее характерных особенностей жидкостей является способность изменять свою форму, под действием внешних сил. Это свой­ство жидкости объясняется скольжением ее молекул относительно друг друга. Одна и та же сила создает в разных жидкостях разные скорости пе­ремещения слоев, отстоящих один от другого на одинаковые расстояния. Однако способность молекул к скольжению не бесконечно велика, поэто­му Ньютон рассматривает вязкость как «недостаток скольжения». Обычно вязкостью иливнутренним трением называют свойство жидкости сопро­тивляться взаимному перемещению ее частиц, вызываемому действием приложенной к жидкости силы.

Явление внутреннего трения в жидкости с ее вязкостью было связа­но Ньютоном известной формулой

(1.10)

где t - напряжение внутреннего трения; dv/ dR - градиент скорости по радиусу трубы или относительное изменение скорости по направлению, перпендикулярному к направлению течения, т.е. приращением скорости на единицу длины нормали; h — коэффициент (касательное усилие на единицу площади, приложенное к слоям жидкости, отстоящим друг от друга на расстоянии, равном единице длины, при единичной разности скоростей между ними).

Внутреннее трение, характеризуемое величиной h, немецкий ученый М. Якоб в 1928 году предложил называть динамической вязкостью. В тех­нической литературе за hутвердилось наименование абсолютной вязкости, так как эта величина выражается в абсолютных единицах. Однако в абсо­лютных единицах, можно выражать также и единицы кинематической и удельной вязкости. Термин «динамическая вязкость» соответствует физиче­скому смыслу h, так как согласно учению о вязкости h входит в уравнение, связывающее силу внутреннего трения с изменением скорости на единицу расстояния, перпендикулярного к плоскости движущейся жидкости.

Впервые же динамическая вязкость была выведена врачом Пуазейлем в 1842 г. при изучении процессов циркуляции крови в кровеносных сосудах. Пуазейль применил для своих опытов очень узкие капилляры (диаметром 0,03-0,14 мм), т.е. он имел дело с потоком жидкости, движение которого было прямолинейно послойным (ламинарным). Вместе с тем исследователи, работавшие до Пуазейля, изучали закономерность истечения жидкости в более широких капиллярах, т.е. имели дело с возникающим турбулентным (вихревым) истечением жидкости. Проведя серию опытов с капиллярами, соединенными с шарообразным резервуаром, через которые под действием сжатого воздуха пропускался некоторый объем жидкости, определенный отметками, сделанными сверху и снизу резервуара, Пуазейль пришел к сле­дующим выводам: 1) количество жидкости, вытекающее в единицу време­ни, пропорционально давлению при условии, что длина трубки превышает некоторый минимум, возрастающий с увеличением радиуса. 2) количество жидкости, вытекающее в единицу времени, обратно пропорционально дли­не трубки и прямо пропорционально четвертой степени радиуса. Формула Пуазейля в современной редакции выглядит следующим образом:

где h - коэффициент внутреннего трения (динамическая вязкость); Р – давление, при котором происходило истечение жидкости; t - время истечения жидкости в объёме V, L – длина капилляра; r – радиус капилляра.

Единицей динамической вязкости является сила, необходимая для поддержания разности скоростей, равной 1 м/с, между двумя параллель­ными слоями жидкости площадью 1 м² находящимися друг от друга на расстояний 1м, т.е. единицей измерения динамической вязкости в системе СИ является

Н × с/м² или Па × с .

Единица динамической вязкости, выраженная в физической системе измерения СГС, в честь Пуазейля называется Пуазом, т.е. за единицу ди­намической вязкости принимают сопротивление, которое оказывает жид­кость при относительном перемещении двух ее слоев площадью 1 см² , от­стоящих друг от друга на 1 см, под влиянием внешней силы в 1 дн при скорости перемещения в 1см 1с. Динамическую вязкость при температуре t обозначают h_t .

Приближенное совпадение численного значения динамической вяз­кости воды при 20°С с 1 сантиПуазом (сП) дало повод Бингаму предло­жить построить систему единиц - вязкости, в которой исходной единицей является динамическая вязкость воды при 20°С, принимаемая по Бингаму за 1 сП (точнее h₂₀ воды равна 1,0087 сП). Таким образом, для большинст­ва практических измерений с достаточной точностью можно считать, что h₂₀ воды соответствует 1 сП. Это представляет большое удобство в практи­ческой вискозиметрии, для которой большое значение имеют жидкости с постоянными физико - химическими константами, имеющие точно извест­ную вязкость при данной температуре. Из числа относительных обозначе­ний наибольшим распространением пользуется так называемаяудельная вязкость, показывающая, во сколько раз динамическая вязкость, данной жидкости больше или меньше динамической вязкости воды при какой - то условно выбранной температуре. Таким образом, удельная вязкость пред­ставляет собой отвлеченное число.

Величина, обратная динамической вязкости, носит название текуче­сти и обозначается знаком T.

Жидкости, подчиняющиеся линейному закону течения Ньютона, на­зываются ньютоновскими, представляют индивидуальные вещества либо молекулярно - дисперсные смеси или растворы, внутреннее трение (вяз­кость) которых при данных температуре и давлении является постоянным физическим свойством. Вязкость не зависит от условий определения и скорости перемещения частиц (течения), если не создается условий для турбулентного движения.

Однако для коллоидных растворов внутреннее трение значительно изменяется при различных условиях потока, в частности при изменении скорости течения. Аномальное внутреннее трение коллоидных систем принято называтьструктурной вязкостью. В этом случае частицами, ко­торые перемещаются относительно друг друга в потоке, являются не моле­кулы, как в нормальных жидкостях, а коллоидные мицеллы, способные дробиться и деформироваться при увеличении скорости или изменении ус­ловий потока, в результате чего измеряемое внутреннее трение уменьша­ется (либо, наоборот, увеличивается). Большинство жидких нефтепродук­тов не выявляет признаков структурной вязкости в широком температур­ном интервале. Хотя они и представляют собой относительно сложные, ас­социированные жидкости, они не обладают коллоидной структурой, при­знаки которой обнаруживаются для жидких нефтепродуктов .лишь при низких температурах, приближающихся к температурам потери текучести.

В зависимости от температуры, при которой происходит перекачка, одна и та же жидкость может быть и ньютоновской в области высоких температур и неньютоновской в области низких температур. Неньютонов­ские жидкости могут быть разделены на пластичные, псевдопластнчные и дилатантные.

В пластических жидкостях наряду с вязкостью проявляются так же пластические свойства, заключающиеся в наличии некоторого предельного напряжения сдвига t₀ , после достижения, которого только и возникает «те­кучесть» среды. Поведение пластических жидкостей объясняется наличи­ем в них пространственной структуры, достаточно прочной, чтобы сопро­тивляться любому напряжению, не превосходящему t₀ . Если напряжение превышает t₀ , то структура полностью разрушается и жидкость выдает се­бя как обычная ньютоновская, при напряжении, равном (t=t₀ ). Течение пластичных жидкостей подчиняется уравнению Шведова – Бенгама

Это уравнение после почленного деления на dv/ dR можно предста­вить в виде

h₀ =h+h₀ (1.11)

где h₀ - эффективная или кажущаяся вязкость; h - истинная вяз­кость; h₀ - структурная составляющая эффективная вязкость.

Псевдопластичные жидкости не обнаруживают начального напря­жения сдвига и для жидкостей справедлива независимость вида

(1.12)

где k и n — постоянные величины для данной жидкости. Характер­ным для псевдопластичных жидкостей является то, что n всегда меньше единицы.

Дилатантные жидкости, сходны с псевдопластическими тем, что в них тоже нет начального напряжения сдвига. Течение этих жидкостей так­же подчиняется степенному закону (1.12), но показатель n превышает еди­ницу.

У многих жидкостей зависимость между напряжением и градиен­том скорости изменяется во времени и поэтому не может быть выра­жена простыми формулами.

Жидкости, обладающие свойством, изотермического самопроизволь­ного увеличения прочности структуры во времени и восстановления структуры после ее разрушения, называются парафинистые нефти. При технических расчетах, а также при контроле качества нефтей и нефтепро­дуктов широкое распространение получил коэффициент кинематиче­ской вязкости, который представляет собой отношение коэффициента ди­намической вязкости m к плотности жидкости при той же температуре

(1.13)

В физической системе единиц широкое применение имеет единица кинематической вязкости в см² /с (Стокc - Ст.) и мм² /с (сантиСтокс - сСт). Таким образом, 1 Cm представляет собой вязкость жидкости, плотность которой равна 1г /1мл и сила сопротивления которой взаимному перемеще­нию двух слоев жидкости площадью 1 см² , находящихся на расстоянии 1 см один от другого и перемещающихся один относительна другого со скоростью 1 см/с, равна 1 дн.

Вязкость нефтей и нефтепродуктов зависит от температуры, увеличиваясь с ее понижением. Для выражения зависимости вязкости от температуры предложено много различных формул. Наибольшее примене­ние для практических расчетов подучила формула Рейнольдса - Филонова

, (1.14)

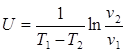(1.15)

где U - коэффициент крутизны вискограммы, 1/К; v*,v - кинематическая вязкость при известной температуре Т_ж и при температуре Т; е - основание натурального логарифма.

Для нахождения коэффициента крутизны вискограммы для данного продукта достаточно знать значения вязкостей при двух температурах Т₁ и Т₂

Динамическая и кинематическая вязкости - это вполне определен­ные физические характеристики, которые, как и все другие величины, вы­ражены в абсолютных единицах и могут быть подставлены в те или другие расчетные формулы. В случаях, когда вязкость применяется не как расчет­ная величина, а как практическая характеристика нефтепродукта, ее при­нято выражать не в абсолютных, а в относительных, или условных, едини­цах.

Подобный способ выражения вязкости является результатом непра­вильного представления о том, что определение динамической и к