Реферат: Формула полной вероятности и формула Бейеса Байеса и их применение
По теореме умножения вероятностей числитель формулы (1) можно представить в виде
P 
= P 
= P (A /Hk )P (Hk )
Для представления знаменателя формулы (1) можно использовать формулу полной вероятности
P (A )
Теперь из (1) можно получить формулу, называемую формулой Байеса :
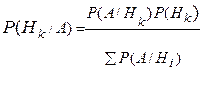
По формуле Байеса исчисляется вероятность реализации гипотезы Hk при условии, что событие А произошло. Формулу Байеса еще называют формулой вероятности гипотез. Вероятность P (Hk ) называют априорной вероятностью гипотезы Hk , а вероятность P (Hk /A ) – апостериорной вероятностью.
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.
Пример. Рассмотрим приведенную выше задачу об электролампах, только изменим вопрос задачи. Пусть покупатель купил электролампу в этом магазине, и она оказалась бракованной. Найти вероятность того, что эта лампа изготовлена на втором заводе. Величина P (H 2 ) = 0,5 в данном случае это априорная вероятность события, состоящего в том, что купленная лампа изготовлена на втором заводе. Получив информацию о том, что купленная лампа бракованная, мы можем поправить нашу оценку возможности изготовления этой лампы на втором заводе, вычислив апостериорную вероятность этого события.
Выпишем формулу Байеса для этого случая
Из этой формулы получаем: P (H 2 /A ) = 15/34. Как видно, полученная информация привела к тому, что вероятность интересующего нас события оказывается ниже априорной вероятности.
3. Задачи с решениями.
Задача 1. В магазин поступила новая продукция с трех предприятий. Процентный состав этой продукции следующий: 20% - продукция первого предприятия, 30% - продукция второго предприятия, 50% - продукция третьего предприятия; далее, 10% продукции первого предприятия высшего сорта, на втором предприятии - 5% и на третьем - 20% продукции высшего сорта. Найти вероятность того, что случайно купленная новая продукция окажется высшего сорта.
Решение. Обозначим через В событие, заключающееся в том, что будет куплена продукция высшего сорта, через 
обозначим события, заключающиеся в покупке продукции, принадлежащей соответственно первому, второму и третьему предприятиям.
Можно применить формулу полной вероятности, причем в наших обозначениях:
Подставляя эти значения в формулу полной вероятности, получим искомую вероятность:
Задача 2. Один из трех стрелков вызывается на линию огня и производит два выстрела. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго - 0,5; для третьего - 0,8. Мишень не поражена. Найти вероятность того, что выстрелы произведены первым стрелком.
Решение. Возможны три гипотезы:
- на линию огня вызван первый стрелок,
- на линию огня вызван второй стрелок,
- на линию огня вызван третий стрелок.
Так как вызов на линию огня любого стрелка равновозможен, то 
В результате опыта наблюдалось событие В - после произведенных выстрелов мишень не поражена. Условные вероятности этого события при сделанных гипотезах равны:
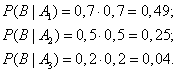
по формуле Байеса находим вероятность гипотезы после опыта:
