Введение 3

1. Формула полной вероятности 4-5

2. Формула Байеса(Бейеса) 5-6

3. Задачи с решениями 7-11

4. Основные сферы применения формулы Байеса(Бейеса) 11

Заключение 12

Литература 13

Введение

Теория вероятностей является одним из классических разделов математики. Она имеет длительную историю. Основы этого раздела науки были заложены великими математиками. Назову, например, Ферма, Бернулли, Паскаля.
Позднее развитие теории вероятностей определились в работах многих ученых.
Большой вклад в теорию вероятностей внесли ученые нашей страны:
П.Л.Чебышев, А.М.Ляпунов, А.А.Марков, А.Н.Колмогоров. Вероятностные и статистические методы в настоящее время глубоко проникли в приложения. Они используются в физике, технике, экономке, биологии и медицине. Особенно возросла их роль в связи с развитием вычислительной техники.

Например, для изучения физических явлений производят наблюдения или опыты. Их результаты обычно регистрируют в виде значений некоторых наблюдаемых величин. При повторении опытов мы обнаруживаем разброс их результатов. Например, повторяя измерения одной и той же величины одним и тем же прибором при сохранении определенных условий (температура, влажность и т.п.), мы получаем результаты, которые хоть немного, но все же отличаются друг от друга. Даже многократные измерения не дают возможности точно предсказать результат следующего измерения. В этом смысле говорят, что результат измерения есть величина случайная. Еще более наглядным примером случайной величины может служить номер выигрышного билета в лотерее. Можно привести много других примеров случайных величин. Все же и в мире случайностей обнаруживаются определенные закономерности. Математический аппарат для изучения таких закономерностей и дает теория вероятностей.
Таким образом, теория вероятностей занимается математическим анализом случайных событий и связанных с ними случайных величин.

1. Формула полной вероятности.

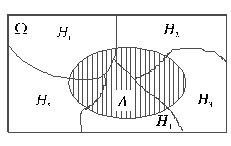
Пусть имеется группа событий H ₁ , H ₂ ,..., H_n , обладающая следую­щими свойствами:

1) все события попарно несовместны: H_i H_j =Æ; i , j =1,2,...,n ; i ¹ j ;

2) их объединение образует пространство элементарных исходов W:

W = .

Рис.8

В этом случае будем говорить, что H ₁ , H ₂ ,...,H_n образуют полную группу событий . Такие события иногда называют гипотезами .

Пусть А – некоторое событие: А ÌW (диаграмма Венна представлена на рисунке 8). Тогда имеет место формула полной вероятности:

P (A ) = P (A /H ₁ )P (H ₁ ) + P (A /H ₂ )P (H ₂ ) + ...+P (A /H_n )P (H_n ) =

Доказательство. Очевидно: A = , причем все события (i = 1,2,...,n ) попарно несовместны. Отсюда по теореме сложения вероятностей получаем

P (A ) = P () + P () +...+ P (

Если учесть, что по теореме умножения P () = P (A/H _i )P (H _i ) (i = 1,2,...,n ), то из последней формулы легко получить приведенную выше формулу полной вероятности.

Пример . В магазине продаются электролампы производства трех заводов, причем доля первого завода - 30%, второго - 50%, третьего - 20%. Брак в их продукции составляет соответственно 5%, 3% и 2%. Какова вероятность того, что случайно выбранная в магазине лампа оказалась бракованной.

Пусть событие H ₁ состоит в том, что выбранная лампа произведена на первом заводе, H ₂ на втором, H ₃ - на третьем заводе. Очевидно:

P (H ₁ ) = 3/10, P (H ₂ ) = 5/10, P (H ₃ ) = 2/10.

Пусть событие А состоит в том, что выбранная лампа оказалась бракованной; A/H_i означает событие, состоящее в том, что выбрана бракованная лампа из ламп, произведенных на i -ом заводе. Из условия задачи следует:

P (A / H ₁ ) = 5/10; P (A / H ₂ ) = 3/10; P (A / H ₃ ) = 2/10

По формуле полной вероятности получаем

2. Формула Байеса( Бейеса)

Пусть H ₁ ,H ₂ ,...,H_n - полная группа событий и А Ì W – некоторое событие. Тогда по формуле для условной вероятности

(1)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--