Реферат: Формы представления моделей

Таблицы, рассмотренные в предыдущих примерах, было несложно построить и заполнить. Но иногда их разработка требует не только времени, но и определённых навыков и даже некоторого искусства.

Пример

Рассмотрим основные подходы к составлению школьного расписания. Заметим, что расписание занятий, предназначенное для учеников, будет отличаться от расписания тех же занятий, предназначенного для учителей. Так и должно быть, ведь цели моделирования различны. Как же строится таблица ученического расписания? Итак, задача — организовать учебный процесс так, чтобы выполнить учебный план и не нарушить законов о труде учителя; объектом моделирования является организация учебного процесса; субъектом моделирования — завуч; цель моделирования — определить для каждого класса порядок проведения занятий на каждый день недели и представить его в наглядной форме.

Существенные свойства:

• перечень классов в школе и список учителей;

• для каждого класса — перечень учебных дисциплин, фамилии ведущих их учителей и количество отводимых на них часов в неделю (таблица 5);

• для каждого учителя — перечень классов, название учебной дисциплины, количество часов в неделю (таблица 6);

• перечень учебных кабинетов и их назначение;

• количество и время проведения уроков и перемен в течение дня.

Таблица 5 (фрагмент)

Кл.	Предмет	Час.	Учитель
11а	Литература	4	Иванов В.В.
Алгебра	6	Деева Г.П.
Информатика	2	Летова А.Р.
Физика	3	Петров С.А.

Таблица 6

Учитель	Предмет	Кл.	Час.
Летова А.Р.	Информ.	11а	2
Информ.	116	2
Логика	9к	1
Информ.	9к	2

Заметим, что все эти списки и перечни надо предварительно составить, и они тоже являются информационными моделями табличной формы. Задайте вопрос завучу, как он составляет школьное расписание, и вы узнаете интересные методы формализации при построении моделей табличной формы. Вероятнее всего вы услышите, что составить расписание — дело очень сложное, потому что следует учесть много дополнительных факторов: пожелания учителей и учеников, требования гигиены умственного труда, санитарные требования и пр. Расписание в процессе составления неоднократно изменяется, уточняется, проверяется на непротиворечивость. Например, необходимо постоянно следить, чтобы у одного учителя не было занятий одновременно в двух классах, чтобы у разных классов не было занятий в одном и том же кабинете на одном и том же уроке, чтобы у учащихся не было «окон» и пр.

4. Представление информации в форме графа

Вы, вероятно, имеете представление о компьютерных сетях. Возможно, компьютеры в школьном кабинете информатики объединены в локальную сеть или вы работали в Интернете, или пользовались услугами электронной почты. Понятно, что сеть образуется только тогда, когда компьютеры каким-либо образом соединены между собой каналами передачи данных. Размещение абонентов сети (подключённых к ней компьютеров или других систем автоматической обработки данных) и способ их соединения друг с другом называется конфигурацией сети. Продемонстрировать различные типы конфигураций вычислительных сетей можно, например, с помощью таких информационных моделей, как графы. Граф — совокупность точек, соединённых между собой линиями. Точки называют вершинами графа. Они могут изображаться точками, кружочками, прямоугольниками и пр. Линии, соединяющие вершины, называются дугами (если задано направление от одной вершины к другой) или рёбрами (если направленность двусторонняя, то есть направления равноправны). Две вершины, соединенные ребром (дугой) называются смежными. Вершины и рёбра графа могут характеризоваться некоторыми числовыми величинами. Например, может быть известна длина ребра или «стоимость прохождения» по нему. Такие характеристики называют весом, а граф называется взвешенным.

Граф однозначно задан, если заданы множество его вершин, множество рёбер (дуг) и указано, какие вершины какими рёбрами (дугами) соединены и, возможно, указаны веса вершин и рёбер (дуг). Определение всех этих элементов и составляет суть формализации в этом случае.

Пример

На рис.3 представлены различные типы конфигураций локальных вычислительных сетей (ЛВС), являющиеся информационными моделями структур ЛВС, представленными в виде графов:

• шинная конфигурация, когда к незамкнутому каналу с некоторыми интервалами подключаются отдельные абоненты (К) информация от абонента-источника распространяется по каналу в обе стороны;

• кольцевая конфигурация, когда каждый абонент непосредственно связан с двумя соседними абонентами, а информация передаётся по замкнутому кольцу, чаще всего в одну сторону;

• звездообразная конфигурация, в центре которой находится центральный коммутатор (ЦК), который последовательно опрашивает абонентов и предоставляет им право на обмен данными;

• древовидная конфигурация образуется подсоединением нескольких простых каналов связи к одному магистральному;

• полносвязная конфигурация обеспечивает выбор наиболее быстрого маршрута связи между абонентами и удобна там, где управление оказывается достаточно сложным.

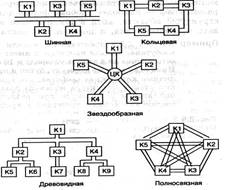
Рис.3 Различные типы конфигураций локальных вычислительных сетей

Наиболее наглядно граф задаётся рисунком. Однако не все детали рисунка одинаково важны. В частности, несущественны геометрические свойства рёбер (длина, кривизна и так далее), форма вершин (точка, кружок, квадрат, овал и пр.) и взаимное расположение вершин на плоскости. Так, на рис.4 представлены два изображения одного и того же графа. Все вершины и ребра часто задаётся в виде сопровождающей надписи на вершине или линии, но, введя условные обозначения, их можно задать формой или цветом вершины, толщиной, типом или цветом линии и т. п.

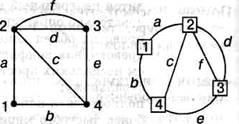
Рис. 4 Различные изображения одного и того же графа

Информационную модель в форме графа можно использовать для наглядного представления взаимосвязей, существующих между элементами объекта моделирования. Таким образом, граф — наиболее удобная форма для моделирования структуры объекта, хотя в такой форме можно моделировать и внешний вид, и поведение объекта.

Пример