Реферат: Фотоэлектронная эмиссия

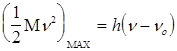. (3)

Соотношение Эйнштейна (2) лежит в основе ряда фотоэлектрических методов измерения работы выхода фотокатодов. Например, величену c можно определить, измеряя в сферическом конденсаторе (при ) истиную разность потенциалов катод-коллектор,при которой фототок прекращается . Действительно (с учетом контактной разности потенциалов )

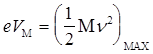
следовательно,

т.е. при заданом можем вычислить и далее определить из соотношения

или

т.е.

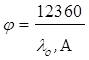(4)

Закон Эйнштейна как показала эксперементальная проверка, строго выполняется для любых

фотокатодов, в том числе и для сложных ) Для металов закон Эйнштейна впервые подвердил на опыте Р.Милликен, но наибольшее точное исследование было выполнено П.И.Лукирским и С.С. Прилежаевым, которые применили метод тормозящего поля между сферическими электродами, ранее разработаный П.И.Лукирским. Пусть в системе двух концентрических сферических электродов эмиттером служит внутернняя сфера рассмотрим электрон,вылетевший из точки А под прямым углом к радиусу ОА, и предположим сначала, что напряжение между электродами отсуствует. Электрон движется с постоянной скоростью, и по мере приближения к наружному электроду радиальная составляющая скорости растет , а составляющая, перпендикулярная к радиусу , уменьшается, и в точке прибытия В

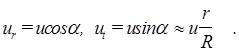(5)

Если между электродами приложено напряжение, то электрическое поле радиально и оно изменяет только а остается такой же, как в отсуствие поля. Значит, в точке прибытия тангециального электрона энергия, связанная с составляющей , равна

, (6)

где К­—полная энергия электрона. Формула дает часть полной энергии, которая не измеряется

в методе тормозящего поля между сферическими электродами. Если ,то и, подавно,, и измеряемая часть энергии равна

, (7)

т.е. при можно с большой степенью точностью измерять распределения полных энергий электронов. Неизмеряемая часть энергии будет наибольшей для электронов, начальная скорость которых направлена по касательной к поверхности эмиттера.Для всех других электронов ошибка будет еще меньше. Формула (7) остается верной и для системы, в которой внутренняя сфера заменена несферическим катодом достаточно малого размера. рис. показаны результаты измерения вольт-амперной характеристик для меди при трех длинах волн. Из спектрально разложенного потока излучения выделяются монохроматический пучок лучей, который направляется на внутерннюю сферу. Ток (очень слабый) измеряется электромером. Форму измеренных вольт-амперных характеристик истолковать нетрудно. Горизонтальный участок - это ток насыщения, текущий в ускоряющем поле. На рис.4 масштаб выбран так, что ордината, избражающая ток насыщения для всех длин волн, одинакова.В точке, где начинается понижение кривых, происходит переход от ускоряющего поля к тормозящему, и в этой точке напряжение батареи компенсирует контактную разность потенциаллов и истиное напряжение

.

Для точек пересечения характерсеик с осью абсцисс выполняется соотношение

_зап Ф_эм

где U_зап - величина запирающего напряжения и Ф_эм - работа выхода эмиттера. Таким образом, на основании закона Эйнштейна задерживающий потенциал, при котором ток прекращается, лиенйно зависит от частоты , причем по углу наклона прямой можно определитьh (если е считать известным ). На рис.3 паказаны прямые для Al и Cu ,

Рис 3

причем для H получается 6,61· эрг. сек, т.е. привосходное подтверждение закона Эйнштейна.

вольт-амперная характеристика для Cu Рис 4.

Этот опыт доказывает также, что энергия фотона в металле иожет переходить к одному из свободных электронов. В этом состоит особеность фотоэлектрического поглощения света в металлах. Положение начало вольт-амперной характеристики , т.е. точка ее пересечения с осью абсцисс ---, не зависит от работы выхода металла-эмиттера . Если обозначить напряжение батареи, при котором через U_зб , то